Impulse
Forces produce either acceleration or deceleration on moving bodies, and the greater the force acting on an object, the greater its change in velocity and, hence, the greater its change in momentum. However, changing momentum is also related to how long a time the force acts. If a brief force is applied to a stalled automobile, a change in its momentum is produced . The same force applied over an extended period of time produces a greater change in the automobile's momentum. The quantity of impulse is force × time interval, or in shorthand notation:
where F is the net force on the system, and Δt is the duration of the force.
From Newton's 2nd law:
change in momentum equals the average net external force multiplied by the time this force acts.
Therefore, impulse as defined in the previous paragraph is simply equivalent to p.
A force sustained over a long time produces more change in momentum than does the same force applied briefly. A small force applied for a long time can produce the same momentum change as a large force applied briefly because it is the product of the force and the time for which it is applied that is important. Impulse is always equal to change in momentum and is measured in Ns (Newton seconds), as both force and the time interval are important in changing momentum.
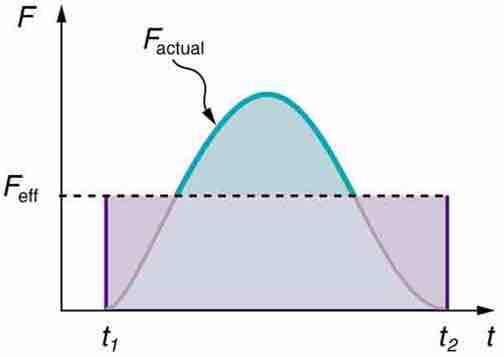
Our definition of impulse includes an assumption that the force is constant over the time interval Δt. Forces are usually not constant. Forces vary considerably even during the brief time intervals considered. It is, however, possible to find an average effective force Feff that produces the same result as the corresponding time-varying force. shows a graph of what an actual force looks like as a function of time for a ball bouncing off the floor. The area under the curve has units of momentum and is equal to the impulse or change in momentum between times t1 and t2. That area is equal to the area inside the rectangle bounded by Feff, t1, and t2. Thus, the impulses and their effects are the same for both the actual and effective forces. Equivalently, we can simple find the area under the curve F(t) between t1 and t2 to compute the impulse in mathematical form:
Force vs. Time
A graph of force versus time with time along the x-axis and force along the y-axis for an actual force and an equivalent effective force. The areas under the two curves are equal.