Conservation of Energy and Momentum

At this point we will expand our discussion of inelastic collisions in one dimension to inelastic collisions in multiple dimensions. It is still true that the total kinetic energy after the collision is not equal to the total kinetic energy before the collision. While inelastic collisions may not conserve total kinetic energy, they do conserve total momentum .

We will consider an example problem in which one mass $(m_1)$ slides over a frictionless surface into another initially stationary mass $(m_2)$. Air resistance will be neglected . The following things are known:

$m_1 = 0.250 kg$,

$m_2 = 0.400 kg$,

$v_1=2.00\;m/s$,

$v{}'_1=1.50\;m/s$,

$v_2=0\;m/s$,

$\theta {}'_1 =45.0^\circ$,

where $v_1$ is the initial velocity of the first mass, $v{}'_1$ is the final velocity of the first mass, $v_2$ is the initial velocity of the second mass, and $\theta {}'_1$ is the angle between the velocity vector of the first mass and the x-axis.

The object is to calculate the magnitude and direction of the velocity of the second mass. After this, we will calculate whether this collision was inelastic or not.

Since there are no net forces at work (frictionless surface and negligible air resistance), there must be conservation of total momentum for the two masses. Momentum is equal to the product of mass and velocity. The initially stationary mass contributes no initial momentum. The components of velocities along the x-axis have the form $v \cdot cos \theta $, where θ is the angle between the velocity vector of the mass of interest and the x-axis.

Expressing these things mathematically:

$m_1v_1=m_1v{}'_1\cdot cos(\theta_1)+m_2v{'}_2\cdot cos(\theta_2)$. (Eq. 2)

The components of velocities along the y-axis have the form v \cdot sin θ, where θ is the angle between the velocity vector of the mass of interest and the x-axis. By applying conservation of momentum in the y-direction we find:

$0=m_1v{}'_1\cdot sin(\theta_1)+m_2v{'}_2\cdot sin(\theta_2)$. (Eq. 3)

If we divide Eq. 3 by Eq. 2, we will find:

$tan{\theta_2}=\frac{v{}'_1\cdot sin\theta_1}{v{}'_1cos\theta \theta _1-v_1}$(Eq. 4)

Eq. 4 can then be solved to find $\theta_2$approx. 312º.

Now let' use Eq. 3 to solve for $v{}'_2$. Re-arranging Eq. 3, we find:

$v{}'_2=\frac{-m_1v{}'_1\cdot sin\theta_1 }{m_2\cdot sin\theta_2}$.

After plugging in our known values, we find that $v{}'_2= 0.886\;m/s$.

We can now calculate the initial and final kinetic energy of the system to see if it the same.

Initial Kinetic Energy =$\frac{1}{2}m_1\cdot v_{1}^2+\frac{1}{2}m_2\cdot v_{2}^2 = 0.5 J$.

Final Kinetic Energy = $\frac{1}{2}m_1\cdot {v{}'_{1}}^2+\frac{1}{2}m_2\cdot {v{}'_{2}}^2\approx 0.43 J$.

Since these values are not the same we know that it was an inelastic collision.

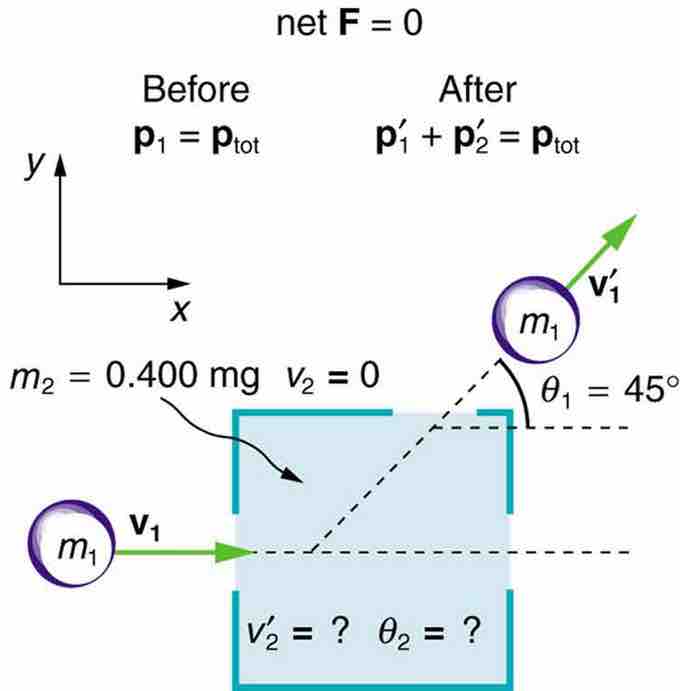
Collision Example

This illustrates the example problem in which one mass collides into another mass that is initially stationary.