Motion of the Center of Mass

We can describe the translational motion of a rigid body as if it is a point particle with the total mass located at the center of mass (COM). In this Atom. we will prove that the total mass (M) times the acceleration of the COM (a_COM), indeed, equals the sum of external forces. That is,

$M \cdot \textbf{a}_{COM} = \sum \textbf{F}_{ext}$.

You can see that the Newton's 2nd law applies as if we are describing the motion of a point particle (with mass M) under the influence of the external force.

Derivation

From the definition of the center of mass,

$\textbf{r}_{COM} = \frac{\sum_i m_i \textbf{r}_i}{M}$,

we get $M \cdot \textbf{a}_{COM} = \sum m_i \textbf{a}_i$ by taking time derivative twice on each side.

Note that $\sum m_i \textbf{a}_i = \sum \textbf{F}_i$.

In a system of particles, each particle may feel both external and internal forces. Here, external forces are forces from external sources, while internal forces are forces between particles in the system. Since the sum of all internal forces will be 0 due to the Newton's 3rd law,

$\sum \textbf{F}_i = \sum \textbf{F}_{i, ext}$. Therefore, we get $M \cdot \textbf{a}_{COM} = \sum \textbf{F}_{ext}$.

For example, when we confine our system to the Earth and the Moon, the gravitational force due to the Sun would be external, while the gravitational force on the Earth due to the Moon (and vice versa) would be internal. Since the gravitational forces between the Earth and the Moon are equal in magnitude and opposite in direction, they will cancel out each other in the sum (see ).

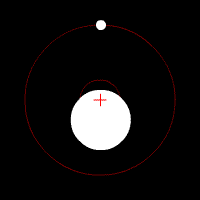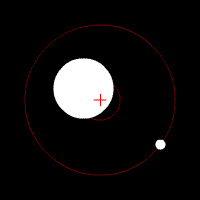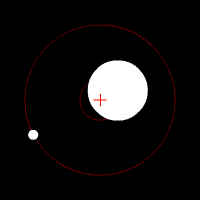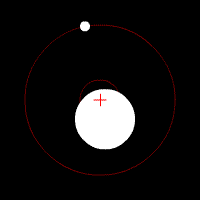
COM of the Earth and Moon

Earth and Moon orbiting a COM inside the Earth. The red cross represents the COM of the two-body system. The COM will orbit around the Sun as if it is a point particle.

Corollary

When there is no external force, the COM momentum is conserved.

Proof: Since there is no external force, $M \cdot \bf{a}_{COM} = 0$. Therefore,

$M \cdot \bf{v}_{COM} = constant$.