Introduction: COM, Linear Momentum, and Collisions
Our study of motion has been limited up to this point. We have referred to particle, object and body in the same way. We considered that actual three dimensional rigid bodies move such that all constituent particles had the same motion (i.e., same trajectory, velocity and acceleration). By doing this, we have essentially considered a rigid body as a point particle.
Center of Mass (COM)
An actual body, however, can move differently than this simplified paradigm. Consider a ball rolling down an incline plane or a stick thrown into air. Different parts of a body have different motions. While translating in the air, the stick rotates about a moving axis, as shown in . This means that such bodies may not behave like a point particle, as earlier suggested.
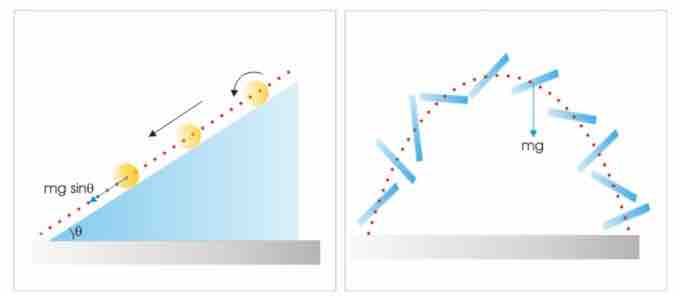
Forces on the COM
Left: The force appears to operate on the COM is "mgsinθ. Right: The force appears to operate on the COM is "mg".
Describing motions of parts or particles that have different motions would be quite complicated to do in an integrated manner. However, such three dimensional bodies in motion have one surprising, simplifying characteristic—a geometric point that behaves like a particle. This point is known as center of mass, abbreviated COM (the mathematical definition of COM will be introduced in the next Atom on "Locating the Center of Mass"). It has the following two characterizing aspects:
- The center of mass appears to carry the whole mass of the body.
- At the center of mass, all external forces appear to apply.
Significantly, the center of a ball (the COM of a rolling ball) follows a straight linear path; whereas the COM of a stick follows a parabolic path (as shown in the figure above). Secondly, the forces appear to operate on the COMs in two cases ("mgsinθ and "mg") as if they were indeed particle-like objects. This concept of COM, therefore, eliminate the complexities otherwise present in attempting to describe motions of rigid bodies.
Describing Motion in a Rigid Body
We can describe general motion of an object (with mass m) as follows:
- We describe the translational motion of a rigid body as if it is a point particle with mass m located at COM.
- Rotation of the particle, with respect to the COM, is described independently.
We "separate" the translational part of the motion from the rotational part. By introducing the concept of COM, the translational motion becomes that of a point particle with mass m. This simplifies significantly the mathematical complexity of the problem.