Section 3
Integrals
By Boundless
An antiderivative is a differentiable function
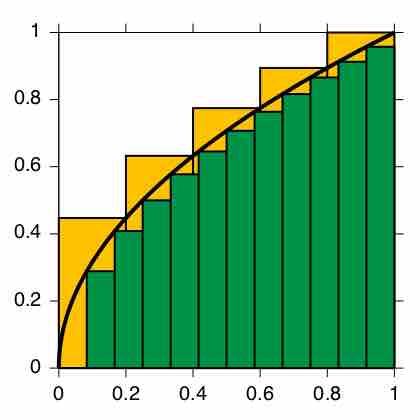
Defined integrals are used in many practical situations that require distance, area, and volume calculations.
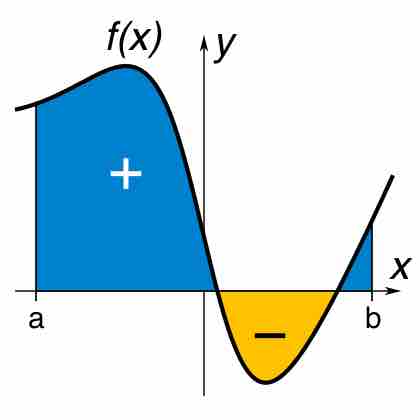
A definite integral is the area of the region in the
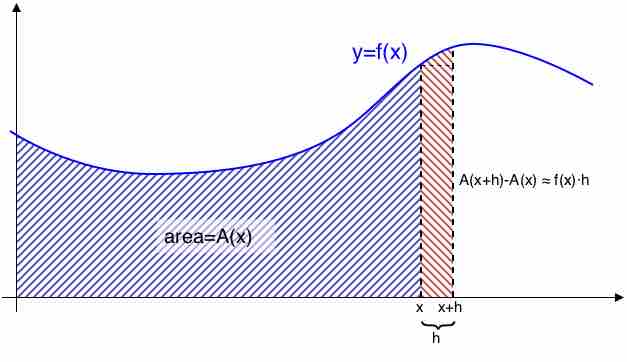
The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function to the concept of the integral.
An indefinite integral is defined as
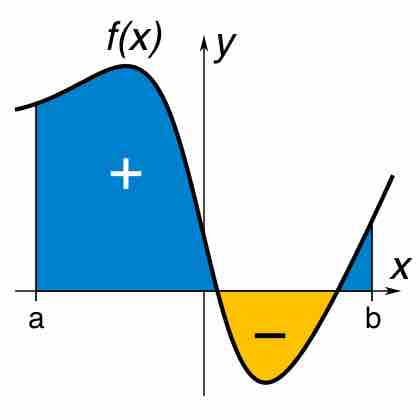
Integration by substitution is an important tool for mathematicians used to find integrals and antiderivatives.
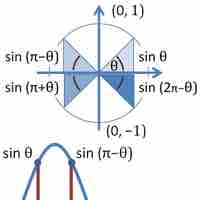
A transcendental function is a function that is not algebraic.
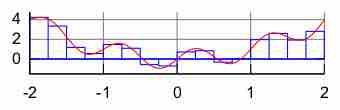
Numerical integration is a method of approximating the value of a definite integral.