Indefinite Integrals and Antiderivatives

As you remember from the atoms on antiderivatives, $F$ is said to be an antiderivative of $f$ if $F'(x) = f(x)$. However, $F$ is not the only antiderivative. We can add any constant $C$ to $F$ without changing the derivative. With this in mind, we define the indefinite integral as follows: $\int f(x)dx = F(x)+ C$ , where $F$ satisfies $F'(x) = f(x)$ and $C$ is any constant.

$f(x)$, the function being integrated, is known as the integrand. Note that the indefinite integral yields a family of functions.

For example, the function $F(x) = \frac{x^3}{3}$ is an antiderivative of $f(x) = x^2$. Since the derivative of a constant is zero, $x^2$ will have an infinite number of antiderivatives, such as $\left ( \frac{x^3}{3} \right ) + 0$, $\left ( \frac{x^3}{3} \right ) + 7$, $\left ( \frac{x^3}{3} \right ) - 42$,$\left ( \frac{x^3}{3} \right ) + 293$, etc. Therefore, all the antiderivatives of $x^2$ can be obtained by changing the value of $C$ in $F(x) = \left ( \frac{x^3}{3} \right ) + C$, where $C$ is an arbitrary constant known as the constant of integration. Essentially, the graphs of antiderivatives of a given function are vertical translations of each other, with each graph's location depending upon the value of $C$.

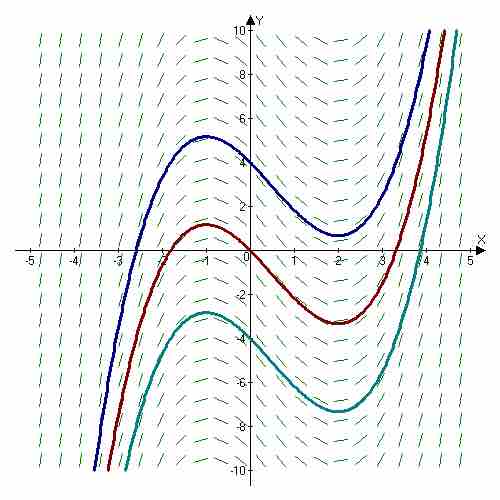
Slope Field

The slope field of $F(x) = \left ( \frac{x^3}{3} \right ) - \left ( \frac{x^2}{2} \right )-x+c$, showing three of the infinitely many solutions that can be produced by varying the arbitrary constant $C$.

Indefinite integrals exhibit the following basic properties.

The Constant Rule for Indefinite Integrals$\int cf(x)dx = c\int f(x)dx$

The Sum Rule for Indefinite Integrals

$\int (f(x)+ g(x)) dx = \int f(x)dx + \int g(x)dx$

The Difference Rule for Indefinite Integrals

$\int (f(x)- g(x)) dx = \int f(x)dx - \int g(x)dx$

Definite Integrals and the Net Change Theorem

Integrating over a specified domain yields what is called a "definite integral" (in that the domain is defined). Integrating over a domain $D$ is written as $\int_{a}^{b} f(x)dx$ if the domain is an interval $[a, b]$ of $x$.

Such a problem can be solved using the net change theorem, which states that the integral of a rate of change is the net change (displacement for position functions): 

$\displaystyle{\int_{a}^{b} f(x)dx = f(b) - f(a)}$

Basically, the theorem states that the integral of or $F'$ from $a$ to $b$ is the area between $a$ and $b$, or the difference in area from the position of $f(a)$ to the position of $f(b)$. This can be applied to find values such as volume, concentration, density, population, cost, and velocity.