The Fundamental Theorem of Calculus

The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function to the concept of the integral.

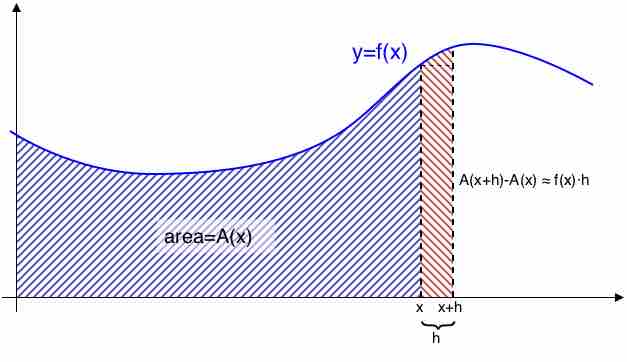
The Fundamental Theorem of Calculus

We can see from this picture that the Fundamental Theorem of Calculus works. By definition, the derivative of $A(x)$ is equal to $\frac{A(x+h)−A(x)}{h}$ as $h$ tends to zero. By replacing the numerator, $A(x+h)−A(x)$, by $hf(x)$ and dividing by $h$, $f(x)$ is obtained. Taking the limit as $h$ tends to zero completes the proof of the Fundamental Theorem of Calculus.

There are two parts to the theorem. Loosely put, the first part deals with the derivative of an antiderivative, while the second part deals with the relationship between antiderivatives and definite integrals.

The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by differentiation. This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.

Let $f$ be a continuous real-valued function defined on a closed interval $[a,b]$. Let $F$ be the function defined, for all $x$ in $[a,b]$, by:

$\displaystyle{F(x) = \int_{a}^{b}f(t)dt}$

Now, $F$ is continuous on $[a,b]$, differentiable on the open interval $( a,b )$, and $F'(x) = f(x)$ for all $x$ in $( a,b )$.

The second part, sometimes called the second fundamental theorem of calculus, allows one to compute the definite integral of a function by using any one of its infinitely many antiderivatives. This part of the theorem has invaluable practical applications, because it markedly simplifies the computation of definite integrals.

Let $f$ and $F$ be real-valued functions defined on a closed interval $[a,b]$ such that the derivative of $F$ is $f$. That is, $f$ and $F$ are functions such that, for all $x$ in $[a,b]$, $F'(x) = f(x)$. If $f$ is a Riemann integrable on $[a,b]$, then:

$\displaystyle{\int_{a}^{b}f(x)dx = F(b) - F(a)}$

The first published statement and proof of a restricted version of the fundamental theorem was by James Gregory (1638–1675). Isaac Barrow (1630–1677) proved a more generalized version of the theorem, while Barrow's student Isaac Newton (1643–1727) completed the development of the surrounding mathematical theory. Gottfried Leibniz (1646–1716) systematized the knowledge into a calculus for infinitesimal quantities and introduced the notation used today.