Concept
Version 7
Created by Boundless
The Fundamental Theorem of Calculus
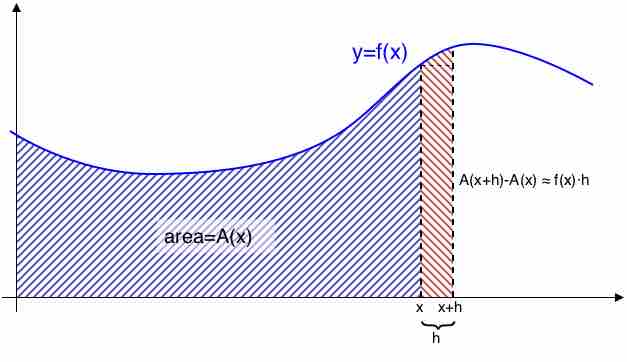
The Fundamental Theorem of Calculus
We can see from this picture that the Fundamental Theorem of Calculus works. By definition, the derivative of
Source
Boundless vets and curates high-quality, openly licensed content from around the Internet. This particular resource used the following sources: