Given a function
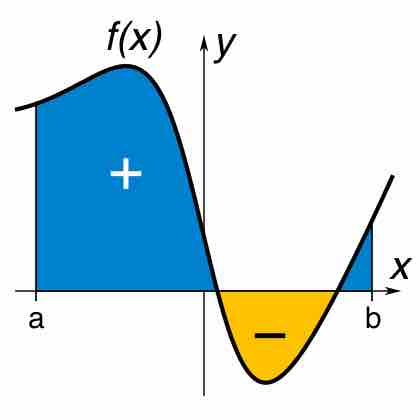
Definite Integral
A definite integral of a function can be represented as the signed area of the region bounded by its graph.
Numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral.
There are several reasons for carrying out numerical integration.
The integrand
A formula for the integrand may be known, but it may be difficult or impossible to find an antiderivative which is an elementary function. An example of such an integrand is
Numerical integration methods can generally be described as combining evaluations of the integrand to get an approximation to the integral.
The integrand is evaluated at a finite set of points called integration points and a weighted sum of these values is used to approximate the integral. The integration points and weights depend on the specific method used and the accuracy required from the approximation. An important part of the analysis of any numerical integration method is to study the behavior of the approximation error as a function of the number of integrand evaluations. A method which yields a small error for a small number of evaluations is usually considered superior. Reducing the number of evaluations of the integrand reduces the number of arithmetic operations involved, and therefore reduces the total round-off error. Also, each evaluation takes time, and the integrand may be arbitrarily complicated. A 'brute force' kind of numerical integration can be done, if the integrand is reasonably well-behaved (i.e. piecewise continuous and of bounded variation), by evaluating the integrand with very small increments.
The simplest method to numerically solve integrals is to use the midpoint or rectangle rule. Draw rectangles which pass through the following point:
The way to do this is as follows:
The area can then be approximated by adding up the areas of the rectangles. Notice that the smaller the rectangles are made, the more accurate the approximation.
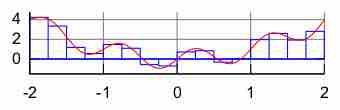
Rectangle Rule
Illustration of the rectangle rule of numerical integration. The value of
The trapezoidal rule is a more accurate method of numerical integration. Instead of taking
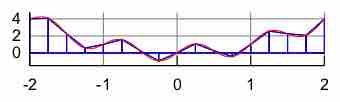
Trapezoidal Rule
Illustration of the trapezoidal rule.
For either one of these rules, we can make a more accurate approximation by breaking up the interval
where the subintervals have the form
Since computers are able to do many arithmetic operations in a small amount of time, they use numerical integration to approximate the values of integrals rather than solving them the way a person would.