Area is a quantity that expresses the extent of a two-dimensional surface or shape, or planar lamina, in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analog of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept).
Area Between Curves
The area between a positive-valued curve and the horizontal axis, measured between two values
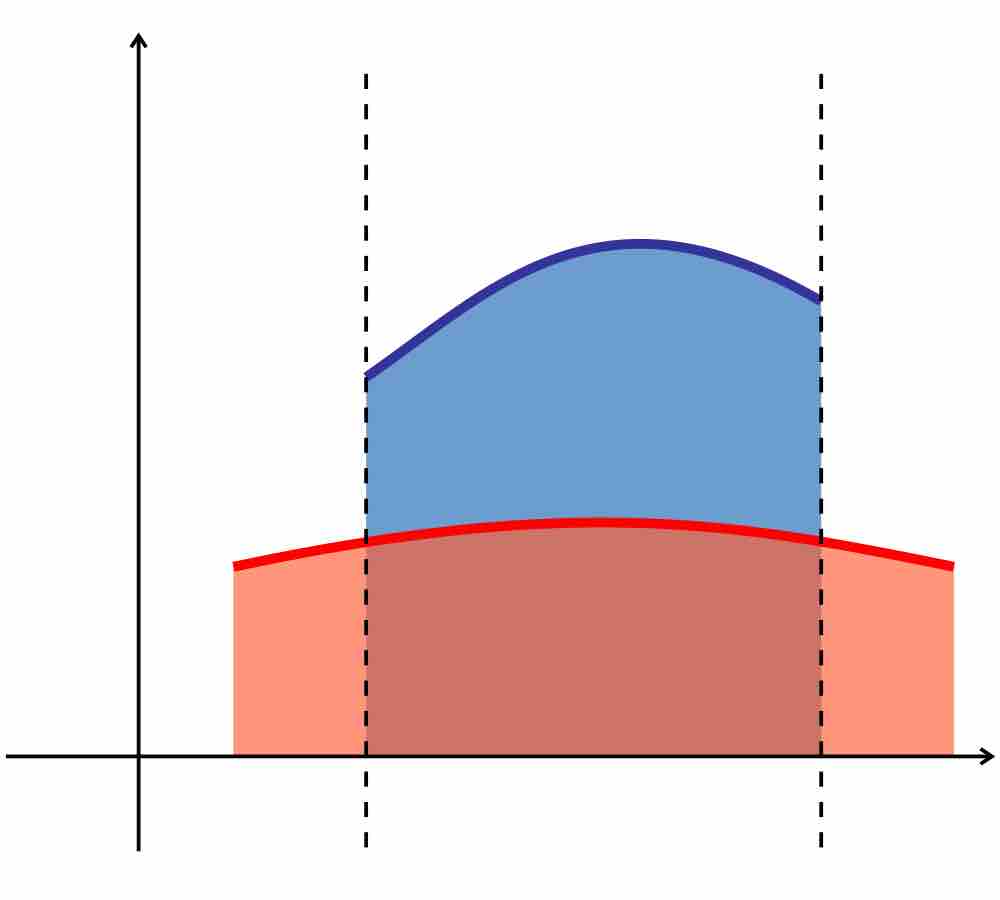
Area Between Two Graphs
The area between two graphs can be evaluated by calculating the difference between the integrals of the two functions.
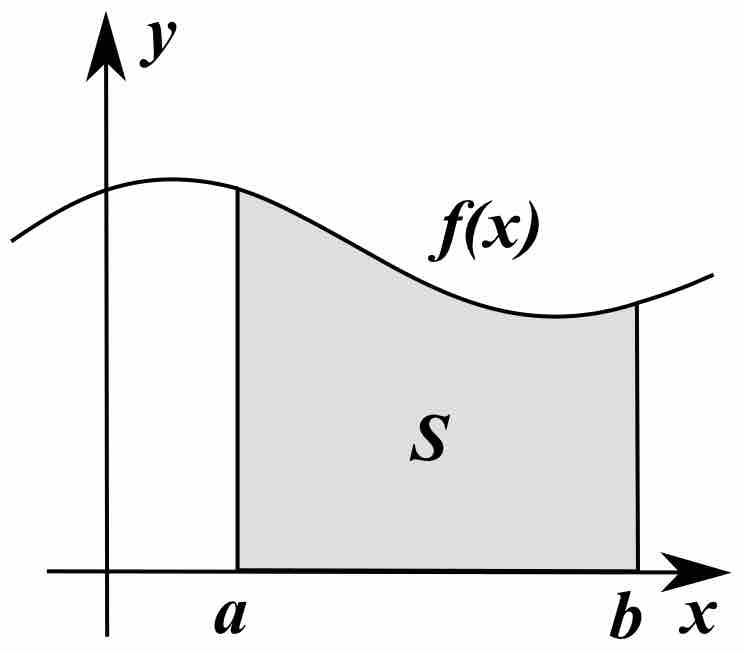
Integration: Area Under a Curve
Integration can be thought of as measuring the area under a curve, defined by
Example
Find the area between the two curves
Two curves,