Area and Distances

Integration is an important concept in mathematics and—together with its inverse, differentiation—is one of the two main operations in calculus.

Integration is connected with differentiation through the fundamental theorem of calculus: if $f$ is a continuous real-valued function defined on a closed interval $[a,b]$, then, once an antiderivative F of f is known, the definite integral of $f$ over that interval is given by$\int_{a}^{b}f(x)dx = F(b) - F(a)$. Definite integrals appear in many practical situations that require distance, area, and volume calculations.

Area

To start off, consider the curve $y = f(x)$ between $0$ and $x=1$ with $f(x) = \sqrt{x}.$

We ask, "What is the area under the function $f$, over the interval from $0$ to $1$? " and call this (yet unknown) area the integral of $f$. The notation for this integral will be:

$\displaystyle{\int_{0}^{1} \sqrt{x} dx}$

As a first approximation, look at the unit square given by the sides $x = 0$ to $x = 1$, $y = f(0) = 0$, and $y = f(1) = 1$. Its area is exactly $1$. As it is, the true value of the integral must be somewhat less. Decreasing the width of the approximation rectangles should yield a better result, so we will cross the interval in five steps, using the approximation points $0$, $\frac{1}{5}$, $\frac{2}{5}$, and so on, up to $1$. Fit a box for each step using the right end height of each curve piece, thus obtaining $\sqrt{\frac{1}{5}}$, $\sqrt{\frac{2}{5}}$, and so on, up to$\sqrt{1} = 1$. Summing the areas of these rectangles, we get a better approximation for the sought integral, namely:

$\displaystyle{\sqrt{\frac{1}{5}} \left ( \frac{1}{5} - 0 \right ) + \sqrt{\frac{2}{5}} \left ( \frac{2}{5} - \frac{1}{5} \right ) + \cdots + \sqrt{\frac{5}{5}} \left ( \frac{5}{5} - \frac{4}{5} \right ) \approx 0.7497}$

Notice that we are taking a finite sum of many function values of $f$, multiplied with the differences of two subsequent approximation points. We can easily see that the approximation is still too large. Using more steps produces a closer approximation, but will never be exact: replacing the $5$ subintervals by twelve as depicted, we will get an approximate value for the area of $0.6203$, which is too small. The key idea is the transition from adding a finite number of differences of approximation points multiplied by their respective function values to using an infinite number of fine, or infinitesimal, steps.

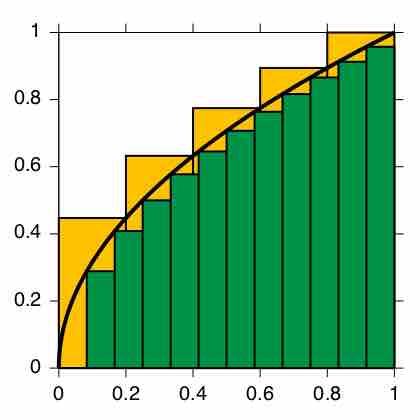
Integral Approximation

Approximations to integral of $\sqrt x$ from $0$ to $1$, with yellow $5$ right samples (above) and green $12$ left samples (below).

Applying the fundamental theorem of calculus to the square root curve, $f(x) = x^{1/2}$, we look at the antiderivative, $F(x) = \frac{2}{3} \cdot x^\frac{3}{2}$, and simply take $F(1) − F(0)$, where $0$ and $1$ are the boundaries of the interval $[0,1]$. So the exact value of the area under the curve is computed formally as:

$\displaystyle{\int_{0}^{1}\sqrt{x}dx = \int_{0}^{1}x^{1/2}dx = F(1) - F(0) = \frac{2}{3}}$

Distance (Finding arc length by Integrating)

If you know the velocity $v(t) $ of an object as a function of time, you can simply integrate $v(t) $ over time to calculate the distance the object traveled. Since this is equivalent to evaluating the area under the curve $v(t) $, we will not discuss more on this.

However, you can also use integrals to calculate length—for example, the length of an arc described by a function $y = f(x)$. Consider an infinitesimal part of the curve $ds$ on the curve (or consider this as a limit in which the change in $s$ approaches $ds$). According to Pythagoras's theorem, $ds^2=dx^2+dy^2$ , from which we can determine:

$\displaystyle{\frac{ds^2}{dx^2}=1+\frac{dy^2}{dx^2}}$

$\displaystyle{ds=\sqrt{1+\left(\frac{dy}{dx}\right)^2}dx}$

$\displaystyle{s = \int_{a}^{b} \sqrt { 1 + [f'(x)]^2 }\, dx}$

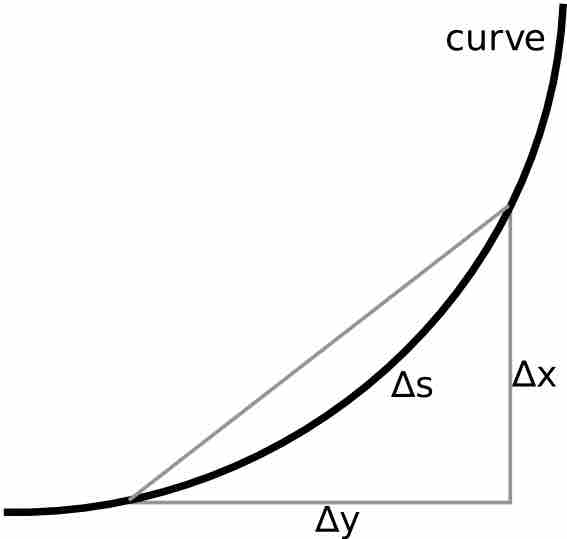
Calculating arc length

For a small piece of curve, $\Delta s$ can be approximated with the Pythagorean theorem.

Equivalently, if a curve is defined parametrically by $x = X(t)$ and $y = Y(t)$, we get:

 $\displaystyle{ds = \sqrt{ \left( \frac{dx}{dt} \right)^2+ \left(\frac{dy}{dt} \right)^2} \cdot dt}$

then its arc length between $t = a$ and $t = b$ is:

 $\displaystyle{s = \int_{a}^{b} \sqrt { [X'(t)]^2 + [Y'(t)]^2 }\, dt}$

Example

For the following  curve described by the parameter $t$:

$\begin{cases} y = t^5 \\ x = t^3 \end{cases}$

the arc length integral for values of $t$ from $-1$ to $1$ is:

 $\displaystyle{\int_{-1}^1 \sqrt{(3t^2)^2 + (5t^4)^2}\,dt}$

$\displaystyle{= \int_{-1}^1 \sqrt{9t^4 + 25t^8}\,dt}$

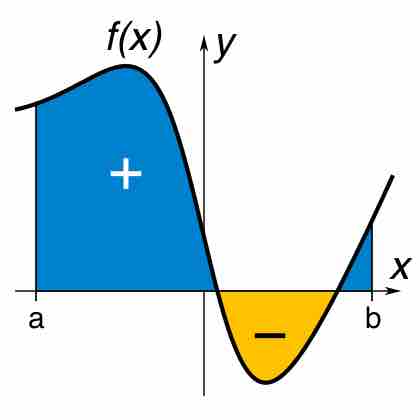
Definite Integral

A definite integral of a function can be represented as the signed area of the region bound by its graph.