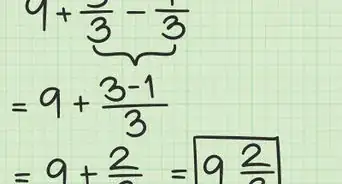Hypothesis testing with z and t statistics
This article was co-authored by wikiHow staff writer, Kyle Smith. Kyle Smith is a wikiHow Technology Writer, learning and sharing information about the latest technology. He has presented his research at multiple engineering conferences and is the writer and editor of hundreds of online electronics repair guides. Kyle received a BS in Industrial Engineering from Cal Poly, San Luis Obispo.
This article has been viewed 2,673 times.
Learn more...
What is the difference really between z and t tests? The main thing is that t tests are used when you don’t know the population variance! You use the Student’s t distribution instead of the standard normal distribution. This wikiHow article compares the t test to the z test, goes over the formulas for t and z, and walks through a couple examples. We'll cover one-sample z and t tests, comparing their key differences.
Things You Should Know
- The main difference is that the t test is used when population variance is unknown.
- Calculate the z statistic using the formula
- Calculate the t statistic using
Steps
Z Test
-
1Use the z statistic to carry out hypothesis testing. The z statistic uses a sampling distribution. Then, it turns it into a standard normal distribution. To calculate the z statistic, use this formula:
- where
- is the sample mean
- is the population mean
- is the sample standard error
- is the population standard deviation
- is the sample size
-
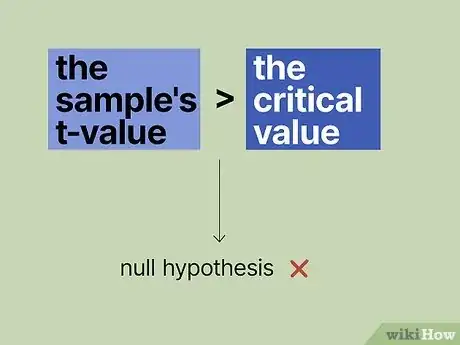
2Make a decision. If the calculated z statistic (also called z score) is greater than the critical z value, you reject the null hypothesis and have significant evidence supporting the alternative hypothesis.
- If you’re testing a proportion, check out our guide on performing hypothesis testing for a proportion.
T Test
-
1Use the t statistic to carry out hypothesis testing. The t statistic uses a sampling distribution. Then, it turns it into the t distribution. To calculate the t statistic, use this formula:
- where
- is the sample mean
- is the population mean
- is the estimated standard error
- is the sample standard deviation
- is the sample size
-
2Make a decision. If the calculated z statistic is greater than the critical z value, you reject the null hypothesis and have significant evidence supporting the alternative hypothesis.
- We cover two-sample t tests in this guide.
Z Test Example
-
1Check out this example of a z test problem. Our population of interest is students who have taken College Class 101 with Dr. Professor. We know that all of Dr. Professor’s past students have averaged 85% on the final, with a standard deviation of 5%. Now we’re interested in seeing if Dr. Professor’s most recent class of 25 students has done significantly better than all her previous classes. The average on the final this year was an 87%, with a standard deviation of 4%.
-
2Set up the hypothesis.
- null hypothesis:
- alternative hypothesis:
-
3Calculate the sample standard error.
-
4Calculate the z statistic.
-
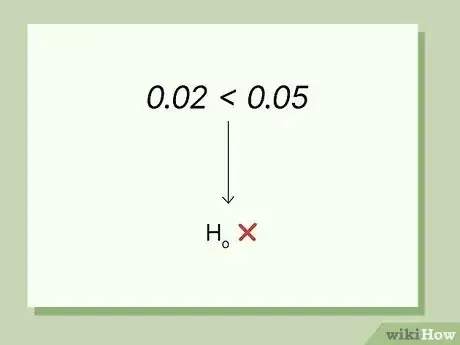
5Find the p-value and interpret the results. Using a z table or an online z calculator, you can find that a z statistic of 2 corresponds with a p-value of about 0.02. Because the p-value is smaller than our alpha of 0.05, we have evidence to reject the null hypothesis that the recent class’s improved exam scores are due to chance alone.
T Test Example
-
1Check out this example of a t test problem. This time we’re comparing the final exam grades of Dr. Professor’s most recent class to the average final exam grade of all students in the school. She wants to know if her students scored significantly higher than the average. We don’t know the standard deviation of all the student’s exam scores. Dr. Professor’s class of 25 students averaged 87% with a standard deviation of 4%, and the school-wide average final exam score was 79%.
-
2Set up the hypothesis.
- null hypothesis:
- alternative hypothesis:
-
3Calculate the estimated standard error.
-
4Calculate the t statistic.
-
5Find the p-value and interpret the results. Using a t table or an online calculator, you can find that a t statistic of 10, with 24 degrees of freedom, corresponds with a p-value of less than .005, which means we have evidence to reject the null hypothesis that Dr. Professor’s class’s final exam score average is no higher than the school-wide average.