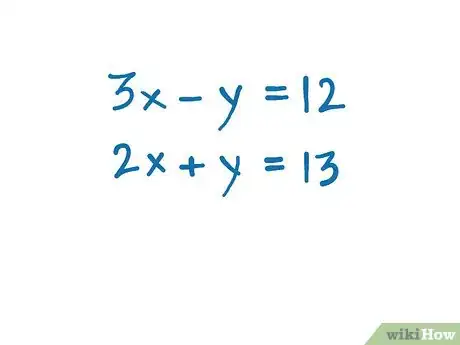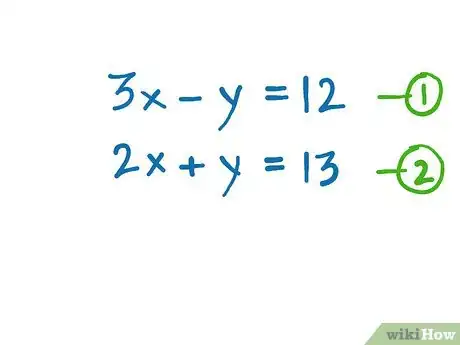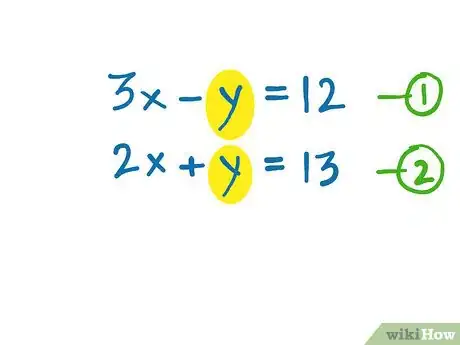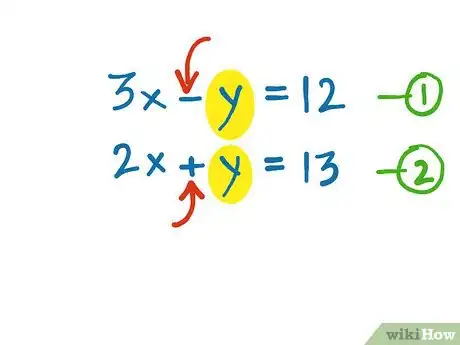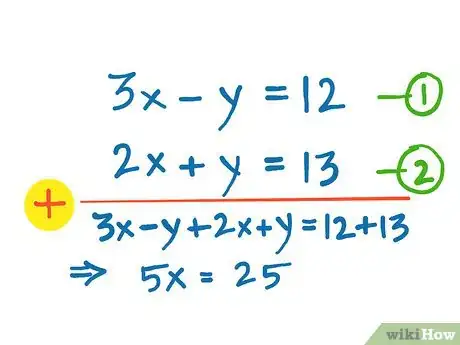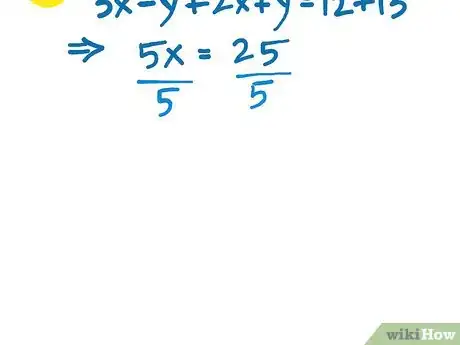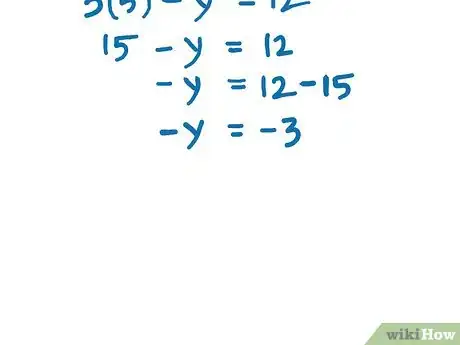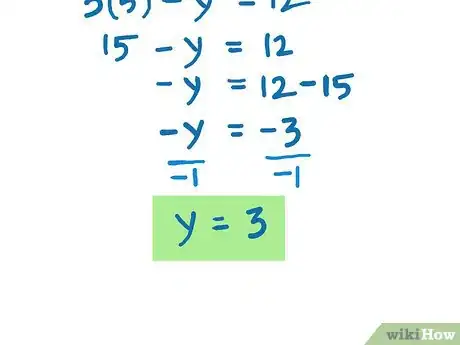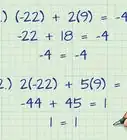X
wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, volunteer authors worked to edit and improve it over time.
This article has been viewed 92,712 times.
Learn more...
Have you ever had a simultaneous problem equation you needed to solve? When you use the elimination method, you can achieve a desired result in a very short time. This article can explain how to perform to achieve the solution for both variables.
Steps
-
1Write down both of the equations that you'll need to solve.[1]
- 3x - y = 12
- 2x + y = 13
-
2Number the equations. 3x - y = 12 as number one, and 2x + y = 13 as number two.[2]Advertisement
-
3Check if both equations have the same variable/unknown term in them.[3]
-
4Look for signs of the unknown variables or terms. Remember subtraction can also be referred to as the addition of a negative number. If the signs are the same, subtract both equations. If they are different then add the equations.[4]
- 3x - y = 12
- + 2x + y = 13
- -------------
- 5x = 25
-
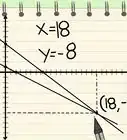
5Solve to find the first unknown variable from the resulting (rather shortened) equation. Divide both sides by the coefficient of the left side. Take 5 to the other side.It will look like this:x = 25/5.[5]
-
625 divided by 5 makes 5 so we have now found the value of "x" which is 5.
-
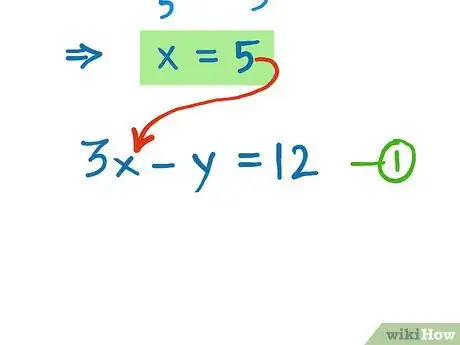
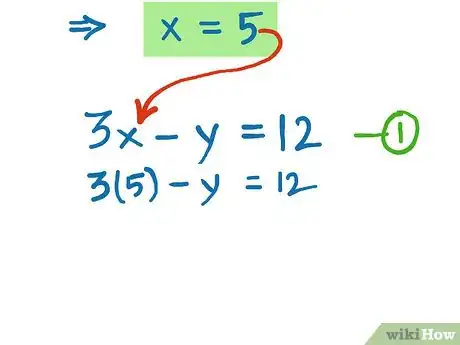
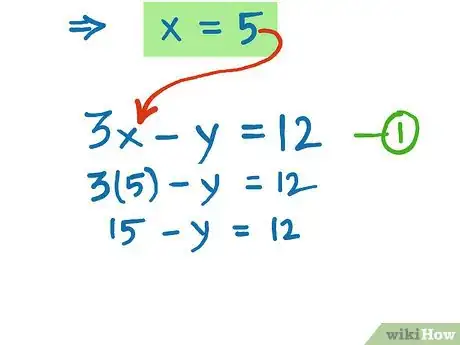
7Find the value of "y". Use the value of x that was obtained above into either equation (but stick with this equation for the time being). Substitute this value of x into the equation.[6]
- 3x - y = 12
- 3(5)-y = 12
- 15 - y = 12
- - y = 12 - 15
- - y = - 3(divide both sides by negative one, will be able to cut both signs)
- y = 3
-
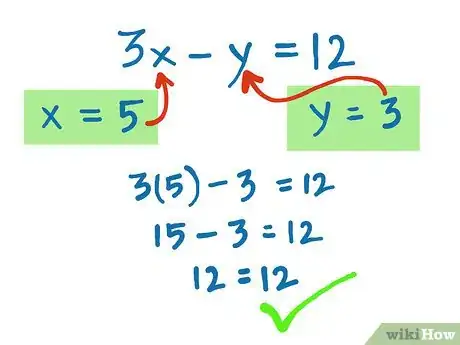
8Check the problem. Substitute both the values into the other equation. If the two side numbers at the very end equal each other, you've correctly solved this system of simultaneous equations.[7]
- 3x - y = 12
- 3(5) - 3 = 12
- 15 - 3 = 12
- 12 = 12
Advertisement
Community Q&A
-
QuestionHow do I find the first term and the constant difference of simultaneous equations?
 DonaganTop Answerer"First term" and "constant difference" do not apply to simultaneous equations. (They are used in arithmetic sequences.)
DonaganTop Answerer"First term" and "constant difference" do not apply to simultaneous equations. (They are used in arithmetic sequences.) -
QuestionIs this useful in all the countries? Where I live, we work our equations very differently.
 DonaganTop AnswererMathematics knows no national boundaries. There is more than one method of solving simultaneous equations, and all methods are known and "useful" in every country. Apparently you were not taught the elimination method in school.
DonaganTop AnswererMathematics knows no national boundaries. There is more than one method of solving simultaneous equations, and all methods are known and "useful" in every country. Apparently you were not taught the elimination method in school. -
QuestionHow do I work with fractions in solving simultaneous equations using elimination method?
 DonaganTop AnswererThe process is the same as outlined above, except that you would have to clear a fraction when solving for a variable. For example, you may see something like 5x/2 = 10, in which case you would just multiply both sides of that equation by 2 and then divide both sides by 5.
DonaganTop AnswererThe process is the same as outlined above, except that you would have to clear a fraction when solving for a variable. For example, you may see something like 5x/2 = 10, in which case you would just multiply both sides of that equation by 2 and then divide both sides by 5.
Advertisement
References
- ↑ https://flexbooks.ck12.org/cbook/ck-12-cbse-math-class-10/section/3.6/primary/lesson/solving-simultaneous-linear-equations-by-elimination/
- ↑ https://www.youtube.com/watch?v=O-rrOPPmFgM
- ↑ https://www.youtube.com/watch?v=7Ja_H6a8ltY
- ↑ https://www.mathsteacher.com.au/year10/ch04_simultaneous/03_elimination_method/elim.htm
- ↑ https://www.bbc.co.uk/bitesize/guides/z9y9jty/revision/1
- ↑ https://www.bbc.co.uk/bitesize/guides/z9y9jty/revision/1
- ↑ https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:systems-of-equations/x2f8bb11595b61c86:solving-systems-elimination/a/elimination-method-review
About This Article
Advertisement