de Broglie and the Bohr Model

Bohr's condition, that the angular momentum is an integer multiple of $\hbar$, was later reinterpreted in 1924 by de Broglie as a standing wave condition. The wave-like properties of matter were subsequently confirmed by observations of electron interference when scattered from crystals. Electrons can exist only in locations where they interfere constructively. How does this affect electrons in atomic orbits? When an electron is bound to an atom, its wavelength must fit into a small space, something like a standing wave on a string. 

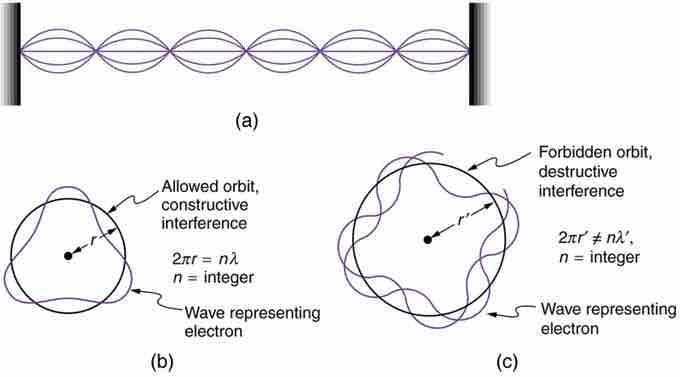
Waves on a String

(a) Waves on a string have a wavelength related to the length of the string, allowing them to interfere constructively. (b) If we imagine the string bent into a closed circle, we get a rough idea of how electrons in circular orbits can interfere constructively. (c) If the wavelength does not fit into the circumference, the electron interferes destructively; it cannot exist in such an orbit.

Allowed orbits are those in which an electron constructively interferes with itself. Not all orbits produce constructive interference and thus only certain orbits are allowed (i.e., the orbits are quantized). By assuming that the electron is described by a wave and a whole number of wavelengths must fit along the circumference of the electron's orbit, we have the equation:

$n\lambda =2\pi r$

Substituting de Broglie's wavelength of $\frac{h}{p}$ reproduces Bohr's rule. Since $\lambda = h/m_ev$, we now have:

 $\displaystyle \frac{nh}{m_ev} = 2\pi r_n$

Rearranging terms, and noting that $L=mvr$ for a circular orbit, we obtain the quantization of angular momentum as the condition for allowed orbits:

$\displaystyle L = m_e v r_n = n \frac{h}{2\pi}, (n=1,2,3...)$

As previously stated, Bohr was forced to hypothesize this rule for allowed orbits. We now realize this as the condition for constructive interference of an electron in a circular orbit.

Accordingly, a new kind of mechanics, quantum mechanics, was proposed in 1925. Bohr's model of electrons traveling in quantized orbits was extended into a more accurate model of electron motion. The new theory was proposed by Werner Heisenberg. By different reasoning, another form of the same theory, wave mechanics, was discovered independently by Austrian physicist Erwin Schrödinger. Schrödinger employed de Broglie's matter waves, but instead sought wave solutions of a three-dimensional wave equation. This described electrons that were constrained to move about the nucleus of a hydrogen-like atom by being trapped by the potential of the positive nuclear charge.