By the early 20th century, research into the interaction of X-rays with matter was well underway. It was observed that when X-rays of a known wavelength interact with atoms, the X-rays are scattered through an angle
In 1923, Compton published a paper in the Physical Review which explained the X-ray shift by attributing particle-like momentum to "photons," which Einstein had invoked in his Nobel prize winning explanation of the photoelectric effect. First postulated by Planck, these "particles" conceptualized "quantized" elements of light as containing a specific amount of energy depending only on the frequency of the light. In his paper, Compton derived the mathematical relationship between the shift in wavelength and the scattering angle of the X-rays by assuming that each scattered X-ray photon interacted with only one electron. His paper concludes by reporting on experiments which verified his derived relation:
where λ\lambda is the initial wavelength, λ′\lambda' is the wavelength after scattering,
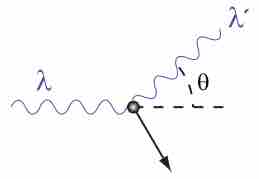
A Photon Colliding with a Target at Rest
A photon of wavelength
Because the mass-energy and momentum of a system must both be conserved, it is not generally possible for the electron simply to move in the direction of the incident photon. The interaction between electrons and high energy photons (comparable to the rest energy of the electron, 511 keV) results in the electron being given part of the energy (making it recoil), and a photon containing the remaining energy being emitted in a different direction from the original, so that the overall momentum of the system is conserved. If the scattered photon still has enough energy left, the Compton scattering process may be repeated. In this scenario, the electron is treated as free or loosely bound. Photons with an energy of this order of magnitude are in the x-ray range of the electromagnetic radiation spectrum. Therefore, you can say that Compton effects (with electrons) occur with x-ray photons.
If the photon is of lower energy, but still has sufficient energy (in general a few eV to a few keV, corresponding to visible light through soft X-rays), it can eject an electron from its host atom entirely (a process known as the photoelectric effect), instead of undergoing Compton scattering. Higher energy photons (1.022 MeV and above, in the gamma ray range) may be able to bombard the nucleus and cause an electron and a positron to be formed, a process called pair production.