Hydrogen Spectra

For decades, many questions had been asked about atomic characteristics. From their sizes to their spectra, much was known about atoms, but little had been explained in terms of the laws of physics. Atomic and molecular emission and absorption spectra have been known for over a century to be discrete (or quantized). Maxwell and others had realized that there must be a connection between the spectrum of an atom and its structure, something like the resonant frequencies of musical instruments. But, despite years of efforts by many great minds, no one had a workable theory. (It was a running joke that any theory of atomic and molecular spectra could be destroyed by throwing a book of data at it, so complex were the spectra.) Following Einstein's proposal of photons with quantized energies directly proportional to their wavelengths, it became even more evident that electrons in atoms can exist only in discrete orbits.

In some cases, it had been possible to devise formulas that described the emission spectra. As you might expect, the simplest atom—hydrogen, with its single electron—has a relatively simple spectrum. The hydrogen spectrum had been observed in the infrared (IR), visible, and ultraviolet (UV), and several series of spectral lines had been observed . The observed hydrogen-spectrum wavelengths can be calculated using the following formula:

$\displaystyle \frac{1}{\lambda} = R(\frac{1}{n_f ^2} - \frac{1}{n_i ^2})$

where $\lambda$ is the wavelength of the emitted EM radiation and $R$ is the Rydberg constant, determined by the experiment to be $R=1.097\cdot 10^7 \text{m}^{-1}$, and $n_f$, $n_i$ are positive integers associated with a specific series.

These series are named after early researchers who studied them in particular depth. For the Lyman series, $n_f = 1$ for the Balmer series, $n_f = 2$; for the Paschen series, $n_f = 3$; and so on. The Lyman series is entirely in the UV, while part of the Balmer series is visible with the remainder UV. The Paschen series and all the rest are entirely IR. There are apparently an unlimited number of series, although they lie progressively farther into the infrared and become difficult to observe as $n_f$ increases. The constant $n_i$ is a positive integer, but it must be greater than $n_f$. Thus, for the Balmer series, $n_f = 2$ and $n_i = 3,4,5,6...$ . Note that $n_i$ can approach infinity. 

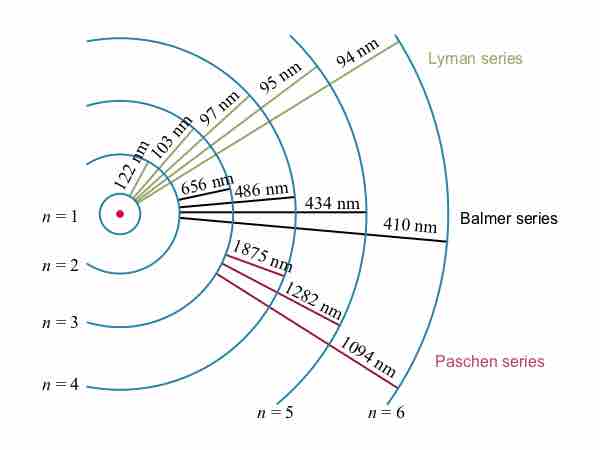
Electron transitions and their resulting wavelengths for hydrogen.

Energy levels are not to scale.

While the formula in the wavelengths equation was just a recipe designed to fit data and was not based on physical principles, it did imply a deeper meaning. Balmer first devised the formula for his series alone, and it was later found to describe all the other series by using different values of $n_f$. Bohr was the first to comprehend the deeper meaning. Again, we see the interplay between experiment and theory in physics. Experimentally, the spectra were well established, an equation was found to fit the experimental data, but the theoretical foundation was missing.