Section 1
Inverse Functions: Exponential, Logarithmic, and Trigonometric Functions
By Boundless
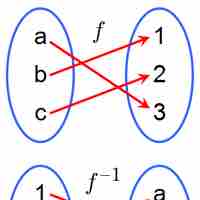
An inverse function is a function that undoes another function.
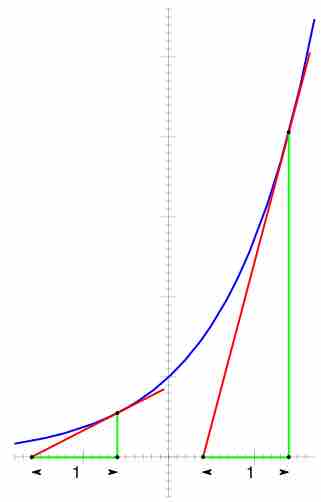
The derivative of the exponential function is equal to the value of the function.
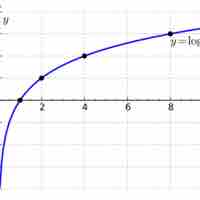
The logarithm of a number is the exponent by which another fixed value must be raised to produce that number.
The general form of the derivative of a logarithmic function is
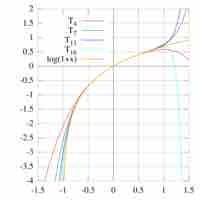
Differentiation and integration of natural logarithms is based on the property
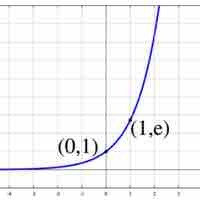
The derivative of the exponential function
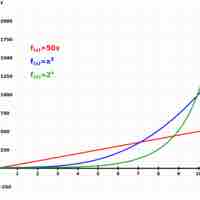
Exponential growth occurs when the growth rate of the value of a mathematical function is proportional to the function's current value.
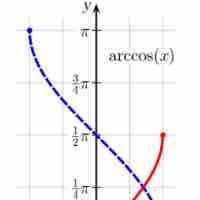
It is useful to know the derivatives and antiderivatives of the inverse trigonometric functions.
Indeterminate forms like
Among all choices for the base