The inverse trigonometric functions are also known as the "arc functions". There are three common notations for inverse trigonometric functions. The arcsine function, for instance, could be written as
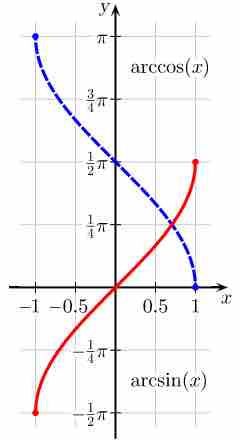
Arcsine and Arccosine
The usual principal values of the
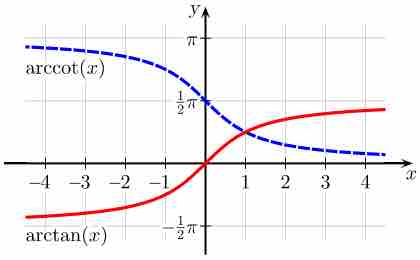
Arctangent and Arccotangent
The usual principal values of the
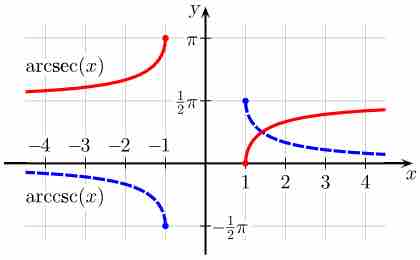
Arcsecant and Arccosecant
Principal values of the
The differentiation of trigonometric functions is the mathematical process of finding the rate at which a trigonometric function changes with respect to a variable.
The integration of trigonometric functions involves finding the antiderivative.
The following is a list of indefinite integrals (antiderivatives) of expressions involving the inverse trigonometric functions.
The derivatives of the inverse trigonometric functions are as follows:
Note that some of these functions are not valid for a range of