Exponential growth occurs when the growth rate of the value of a mathematical function is proportional to the function's current value. Exponential decay occurs in the same way, providing the growth rate is negative.
In the long run, exponential growth of any kind will overtake linear growth of any kind as well as any polynomial growth.
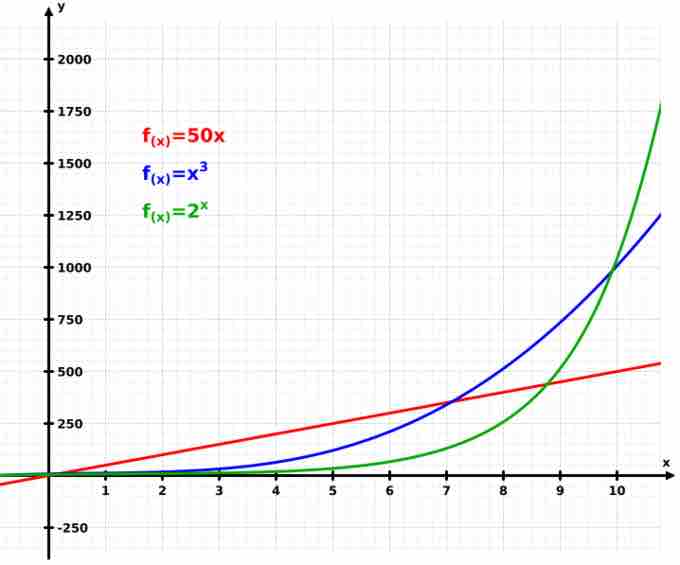
Exponential Growth
This graph illustrates how exponential growth (green) surpasses both linear (red) and cubic (blue) growth.
The formula for exponential growth of a variable
where
A quantity
where the constant
If
Let's assume that a species of bacteria doubles every ten minutes. Starting out with only one bacterium, how many bacteria would be present after one hour? The question implies
After one hour, or six ten-minute intervals, there would be sixty-four bacteria.