The importance of the exponential function in mathematics and the sciences stems mainly from properties of its derivative. In particular:
That is to say,
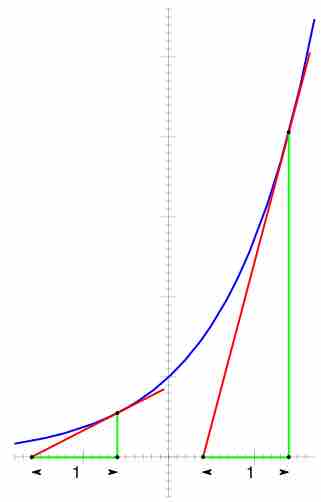
Graph of an Exponential Function
Graph of the exponential function illustrating that its derivative is equal to the value of the function. From any point
Functions of the form
Other ways of saying this same thing include:
- The slope of the graph at any point is the height of the function at that point.
- The rate of increase of the function at
$x$ is equal to the value of the function at$x$ . - The function solves the differential equation
$y' = y $ . -
$e^x$ is a fixed point of derivative as a functional.
If a variable's growth or decay rate is proportional to its size—as is the case in unlimited population growth, continuously compounded interest, or radioactive decay—then the variable can be written as a constant times an exponential function of time. Explicitly for any real constant
Furthermore, for any differentiable function