An inverse function is a function that undoes another function. If an input
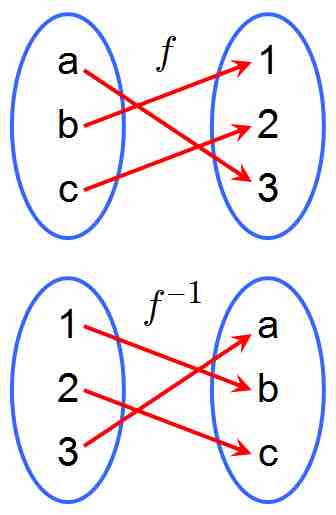
A Function and its Inverse
A function
Instead of considering the inverses for individual inputs and outputs, one can think of the function as sending the whole set of inputs—the domain—to a set of outputs—the range. Let
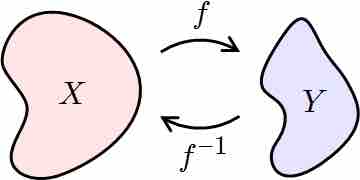
Inverse Functions
If
If
Stated otherwise, a function is invertible if and only if its inverse relation is a function on the range
Example
Let's take the function