Slope-Intercept Form

One of the most common representations for a line is with the slope-intercept form. Such an equation is given by $y=mx+b$, where $x$ and $y$ are variables and $m$ and $b$ are constants.  When written in this form, the constant $m$ is the value of the slope and $b$ is the $y$-intercept.  Note that if $m$ is $0$, then $y=b$ represents a horizontal line. Note that this equation does not allow for vertical lines, since that would require that $m$ be infinite (undefined).  However, a vertical line is defined by the equation $x=c$ for some constant $c$.

Converting an Equation to Slope-Intercept Form

Writing an equation in slope-intercept form is valuable since from the form it is easy to identify the slope and $y$-intercept.  This assists in finding solutions to various problems, such as graphing, comparing two lines to determine if they are parallel or perpendicular and solving a system of equations.

Example

Let's write an equation in slope-intercept form with $m=-\frac{2}{3}$, and $b=3$.  Simply substitute the values into the slope-intercept form to obtain:

$\displaystyle y=-\frac{2}{3}x+3$

If an equation is not in slope-intercept form, solve for $y$ and rewrite the equation.

Example

Let's write the equation $3x+2y=-4$ in slope-intercept form and identify the slope and $y$-intercept. To solve the equation for $y$, first subtract $3x$ from both sides of the equation to get:

$\displaystyle 2y=-3x-4$

Then divide both sides of the equation by $2$ to obtain: 

$\displaystyle y=\frac{1}{2}(-3x-4)$

Which simplifies to $y=-\frac{3}{2}x-2$.  Now that the equation is in slope-intercept form, we see that the slope $m=-\frac{3}{2}$, and the $y$-intercept $b=-2$.

Graphing an Equation in Slope-Intercept Form

We begin by constructing the graph of the equation in the previous example.

Example

We construct the graph the line $y=-\frac{3}{2}x-2$ using the slope-intercept method. We begin by plotting the $y$-intercept $b=-2$, whose coordinates are $(0,-2)$.  The value of the slope dictates where to place the next point.  

Since the value of the slope is $\frac{-3}{2}$, the rise is $-3$ and the run is $2$.  This means that from the $y$-intercept, $(0,-2)$, move $3$ units down, and move $2$ units right.  Thus we arrive at the point $(2,-5)$ on the line. If the negative sign is placed with the denominator instead the slope would be written as $\frac{3}{-2}$, we can instead move up $3$ units and left $2$ units from the $y$-intercept to arrive at the point $(-2,1)$, also on the line.

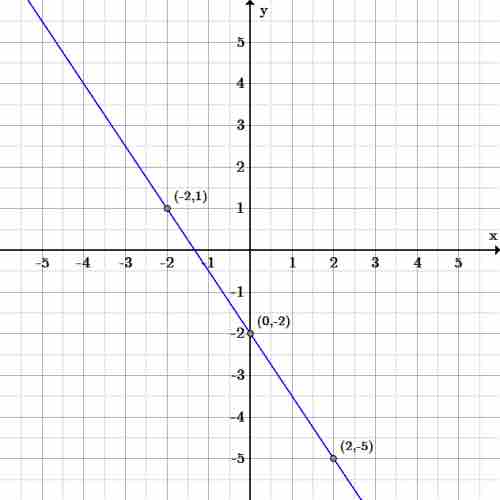
Slope-intercept graph

Graph of the line $y=-\frac{3}{2}x-2$.

Example

Let's graph the equation $12x-6y-6=0$. First we solve the equation for $y$ by subtracting $12x$ to obtain: 

$\displaystyle -6y-6=-12x$   

Next, add $6$ to get:

 $\displaystyle -6y=-12x+6$

Finally, divide all terms by $-6$ to get the slope-intercept form:

$\displaystyle y=2x-1$  

The slope is $2$, and the $y$-intercept is $-1$.  Using this information, graphing is easy.  Start by plotting the $y$-intercept $(0,-1)$, then use the value of the slope, $\frac{2}{1}$, to move up $2$ units and right $1$ unit.

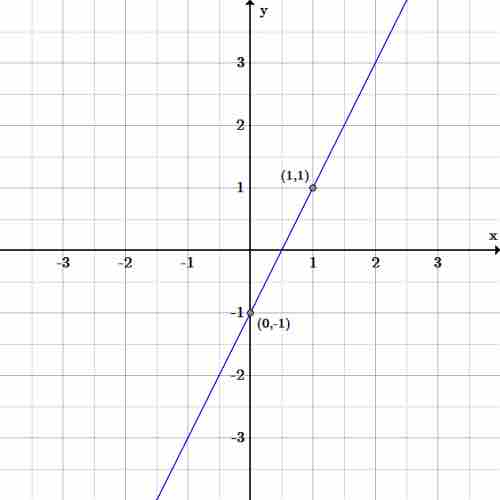
Slope-intercept graph

Graph of the line $y=2x-1$.