Point-Slope Equation
The point-slope equation is a way of describing the equation of a line. The point-slope form is ideal if you are given the slope and only one point, or if you are given two points and do not know what the
Verify Point-Slope Form is Equivalent to Slope-Intercept Form
To show that these two equations are equivalent, choose a generic point
Distribute the negative sign through and distribute
Add
Combine like terms:
Add
Combine like terms:
Therefore, the two equations are equivalent and either one can express an equation of a line depending on what information is given in the problem or what type of equation is requested in the problem.
Example: Write the equation of a line in point-slope form, given a point $(2,1)$ and slope $-4$ , and convert to slope-intercept form
Write the equation of the line in point-slope form:
To switch this equation into slope-intercept form, solve the equation for
Distribute
Add
The equation has the same meaning whichever form it is in, and produces the same graph.
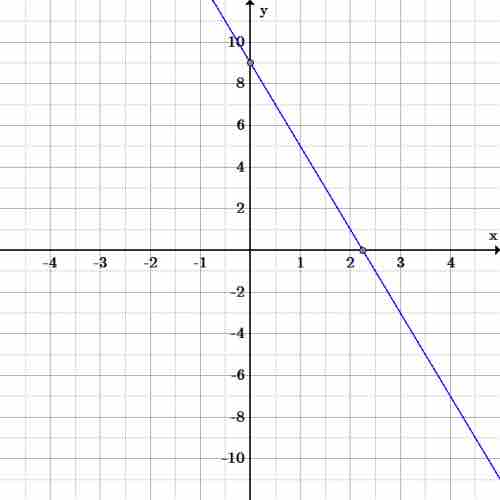
Line graph
Graph of the line
Example: Write the equation of a line in point-slope form, given point $(-3,6)$ and point $(1,2)$ , and convert to slope-intercept form
Since we have two points, but no slope, we must first find the slope:
Substituting the values of the points:
Now choose either of the two points, such as
Be careful if one of the coordinates is a negative. Distributing the negative sign through the parentheses, the final equation is:
If you chose the other point, the equation would be:
Next distribute
Add
Again, the two forms of the equations are equivalent to each other and produce the same line. The only difference is the form that they are written in.