The graph of a linear function is a straight line. Graphically, where the line crosses the $x$-axis, is called a zero, or root.  Algebraically, a zero is an $x$ value at which the function of $x$ is equal to $0$.  Linear functions can have none, one, or infinitely many zeros.  If there is a horizontal line through any point on the $y$-axis, other than at zero, there are no zeros, since the line will never cross the $x$-axis.  If the horizontal line overlaps the $x$-axis, (goes through the $y$-axis at zero) then there are infinitely many zeros, since the line intersects the $x$-axis multiple times.  Finally, if the line is vertical or has a slope, then there will be only one zero.  

Finding the Zeros of Linear Functions Graphically

Zeros can be observed graphically.  An $x$-intercept, or zero, is a property of many functions. Because the $x$-intercept (zero) is a point at which the function crosses the $x$-axis, it will have the value $(x,0)$, where $x$ is the zero.

All lines, with a value for the slope, will have one zero.  To find the zero of a linear function, simply find the point where the line crosses the $x$-axis. 

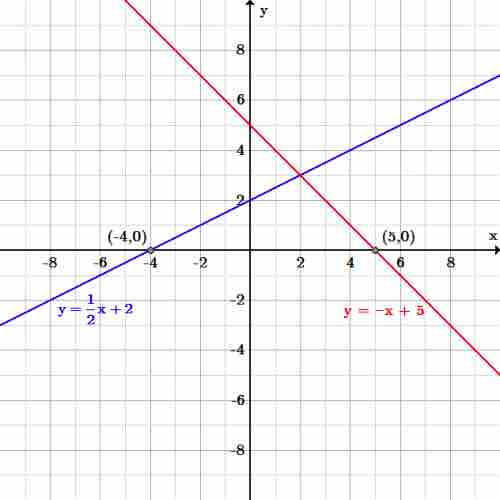
Zeros of linear functions

The blue line, $y=\frac{1}{2}x+2$, has a zero at $(-4,0)$; the red line, $y=-x+5$, has a zero at $(5,0)$.  Since each line has a value for the slope, each line has exactly one zero.  

Finding the Zeros of Linear Functions Algebraically

To find the zero of a linear function algebraically, set $y=0$ and solve for $x$. 

The zero from solving the linear function above graphically must match solving the same function algebraically.  

Example: Find the zero of $y=\frac{1}{2}x+2$ algebraically 

First, substitute $0$ for $y$: 

$\displaystyle 0=\frac{1}{2}x+2$ 

Next, solve for $x$. Subtract $2$ and then multiply by $2$, to obtain: 

$\displaystyle \begin{aligned} \frac{1}{2}x&=-2\\ x&=-4 \end{aligned}$ 

The zero is $(-4,0)$.  This is the same zero that was found using the graphing method.