Chapter 14
Complex Numbers and Polar Coordinates
By Boundless

The polar coordinate system is an alternate coordinate system where the two variables are
Polar and Cartesian coordinates can be interconverted using the Pythagorean Theorem and trigonometry.
Polar coordinates allow conic sections to be expressed in an elegant way.
Some curves have a simple expression in polar coordinates, whereas they would be very complex to represent in Cartesian coordinates.
A complex number has the form
Complex numbers can be added and subtracted by adding the real parts and imaginary parts separately.
Complex numbers can be multiplied using the FOIL algorithm.
Powers of complex numbers can be computed with the the help of the binomial theorem.
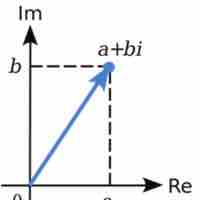
The complex conjugate of the number
Division of complex numbers is accomplished by multiplying by the multiplicative inverse. The multiplicative inverse of
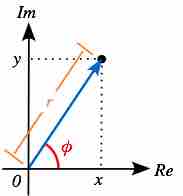
Complex numbers can be represented in polar coordinates using the formula