Introduction of Polar Coordinates
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction.
When we think about plotting points in the plane, we usually think of rectangular coordinates
The reference point (analogous to the origin of a Cartesian system) is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate or radius, and the angle is called the angular coordinate, polar angle, or azimuth. The radial coordinate is often denoted by
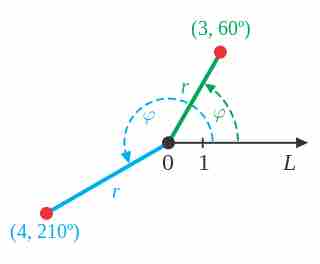
Examples of Polar Coordinates
Points in the polar coordinate system with pole
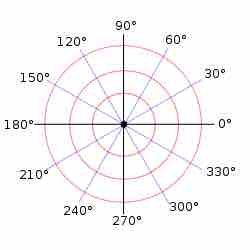
Polar Graph Paper
A polar grid with several angles labeled in degrees
Angles in polar notation are generally expressed in either degrees or radians (
Plotting Points Using Polar Coordinates
The polar grid is scaled as the unit circle with the positive
Plotting a point on a Polar Grid
Plot of the point
Uniqueness of polar coordinates
Adding any number of full turns (