Sometimes it is helpful to think of complex numbers in a different geometric way. The previous geometric idea where the number $z=a+bi$ is associated with the point $(a,b)$ on the usual $xy$-coordinate system is called rectangular coordinates. The alternative way to picture things is called polar coordinates. 

In polar coordinates, the parameters are $r$ and $\phi$. $r$ is how far the point is from the origin, which is usually denoted

 $r=\sqrt{a^2+b^2}=\abs{z}$

The other parameter is the angle $\phi$, which the line from the origin to the point makes with the horizontal, measured in radians. 

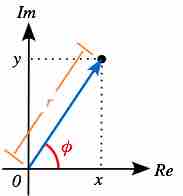
The parameters for polar coordinates

The angle $\phi$ can be deduced using trigonometry from the numbers $a$ and $b$, but we will just consider the following alternative way to write $z=a+bi$. It turns out, due to a theorem of the great mathematician Euler, that we can write $z$ as the complex expression $z=re^{i\phi}$. When written this way, it now becomes easier to multiply and divide complex numbers. 

Multiplying Complex Numbers in Polar Coordinates

So if $z=re^{i\phi}$ and $w=se^{i\theta}$ are complex numbers, then the product of $z$ and $w$ is $zw=rse^{i(\phi+\theta)}$, which comes from simply multiplying as usual for exponential functions. We can then see that the product of $z$ and $w$ is the complex numbers whose distance from the origin is the product of the distances from the origin of $z$ and $w$, and whose angle with the horizontal is the sum of the angles of $z$ and $w$ with the origin.

For example, consider the complex numbers $z=\sqrt2e^{i\pi/4}=1+i$ and $w=\sqrt2e^{3i\pi/4} = -1+i$. 

So $z$ is the complex number which is $\sqrt2$ units from the origin and whose angle with the horizontal is $\pi/4$ radians, which is $45 $ degrees. 

Then $w$ is the number whose distance from the origin is $\sqrt2$ and whose angle with the origin is $3\pi/4$ radians which is $135$ degrees. 

When we multiply $(1+i)(-1+i)$ by FOILing, we obtain $-1+i-i-1=-2$. 

Perhaps more easily we could multiply

 $\begin{aligned} zw&=\sqrt2 e^{i\pi/4}\cdot\sqrt2 e^{3i\pi/4} \\&= 2e^{i\pi} \\&= -2 \end{aligned}$

Realizing that we are getting the number whose distance from the origin is $2$ and whose angle with the horizontal is $\frac{\pi}{4}+\frac{3\pi}{4}=\pi,$ or $180$ degrees. 

Dividing Complex Numbers in Polar Coordinates

Similarly, if $z=re^{i\phi}$ and $w=se^{i\theta}$ then $\frac{z}{w}$ is the result of dividing $\frac{re^{i\phi}}{se^{i\theta}} = \frac{r}{s} e^{i(\phi-\theta)}$

In other words, when dividing by a complex number, the result is a number whose distance from the origin is the quotient of the distances of the two numbers from the origin, and whose angle with the horizontal is the difference of the angles with the horizontal of the two numbers.

For example, If you were to divide $z=\sqrt2e^{i\pi/4} = 1+i$ by $w=\sqrt{2}e^{3i\pi/4}=-1+i$, the result would be:

$\frac{\sqrt2}{\sqrt2} e^{i(\pi/4 -3\pi/4)} = e^{-i\pi/2} = -i$ 

The result is one unit from the origin and at an angle of $-\pi/2$ (or $-90$ degrees) with the horizontal. 

This way of thinking about multiplying and dividing complex numbers gives a geometric way of thinking about those operations.