Complex Conjugates

The complex conjugate (sometimes just called the conjugate) of a complex number $a+bi$ is the complex number $a-bi$. 

Thus, for example, the conjugate of $2+3i$ is $2-3i$ and the conjugate of $1-5i$ is $1+5i$. Since the conjugate of a conjugate is the original complex number, we say that the two numbers are conjugates of each other. 

The symbol for the complex conjugate of $z$ is $\overline{z}$. So, we might write:

 $\overline{3-6i} = 3+6i.$

The Product of Two Conjugates

The product of two conjugates is always a real number. Note that:

$(a+bi)(a-bi)=a^2-abi+abi-b^2i^2=a^2+b^2$ 

This number has a geometric significance.  

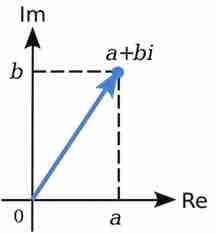
The length of a complex number

The length of the line segment from the origin to the point $a+bi$ is $\sqrt{a^2+b^2}$.  This comes from the Pythagorean Theorem. 

The number $a^2+b^2$ is the square of the length of the line segment from the origin to the number $a+bi$. The number $\sqrt{a^2+b^2}$ is called the length or the modulus of the complex number $z=a+bi$. The symbol for the modulus of $z$ is $\abs{z}$. Thus we can write

 $\begin{aligned} z\overline{z} &= (a+bi)(a-bi)\\&=a^2+b^2\\&=\abs{z}^2 \end{aligned}$

Or in other words:

$\abs{z}=\sqrt{z\overline{z}}$ 

The modulus symbol looks just like the absolute value symbol, which is okay because whenever $b=0$ so that $z=a+bi=a$ is a real number, we have that the conjugate is $a-bi=a$. In this case we have

$\begin{aligned} \sqrt{z\overline{z}} &= \sqrt{a^2}\\&=\abs{a}\\&=\abs{z} \end{aligned}$ 

So the symbol is consistent with the use of the absolute value symbol. 

Complex Roots Come in Conjugate Pairs

One important fact about conjugates is that whenever a complex number is a root of polynomial, its complex conjugate is a root as well. This can be seen in the quadratic formula whenever the discriminant $b^2-4ac$ is negative. 

For example, consider the equation: 

$x^2+x+1=0$

By the quadratic formula, the roots are

$x=\dfrac{-1 \pm \sqrt{1-4\cdot 1 \cdot 1}} {2} $ 

Simplifying gives the two complex numbers $-1/2+(\sqrt{3}/2)i$ and $-1/2-(\sqrt{3}/2)i$ , which are complex conjugates of each other.