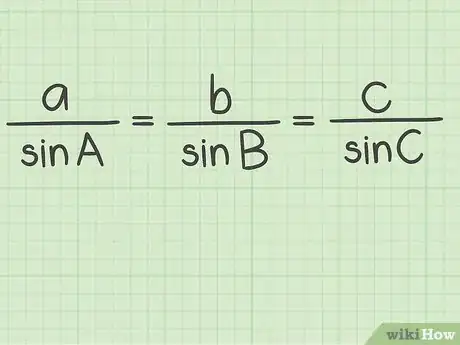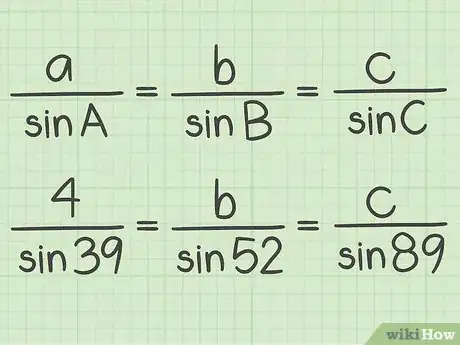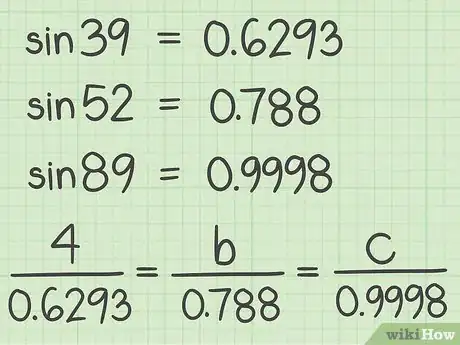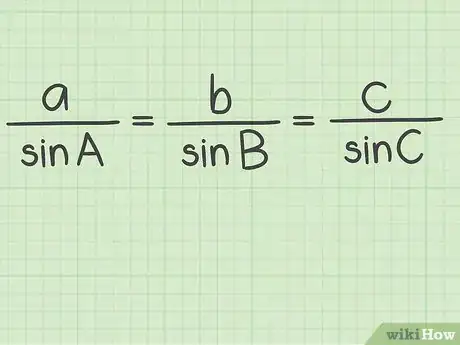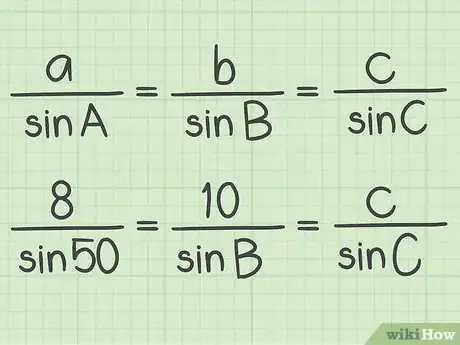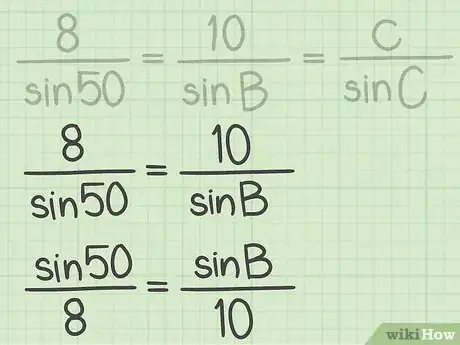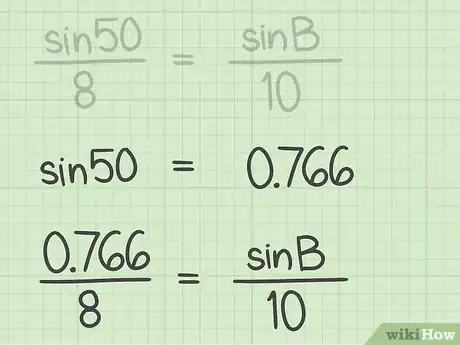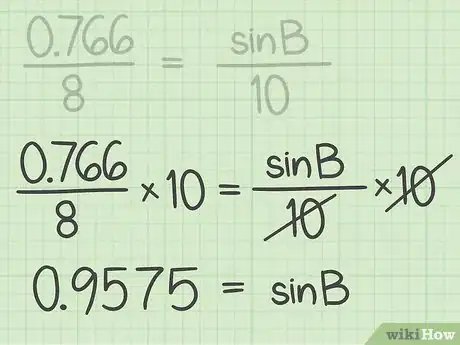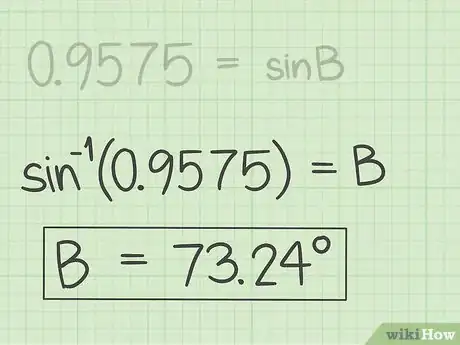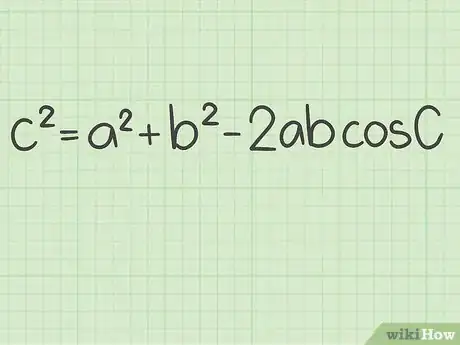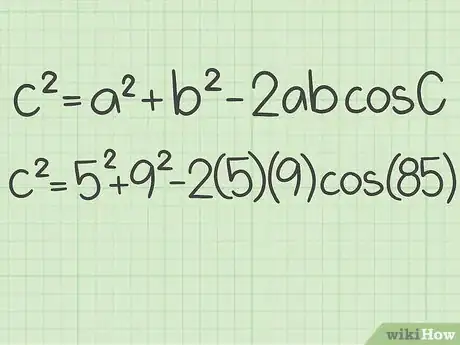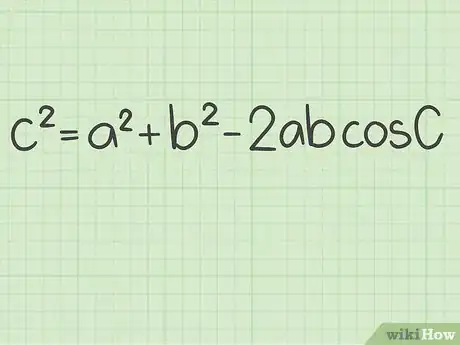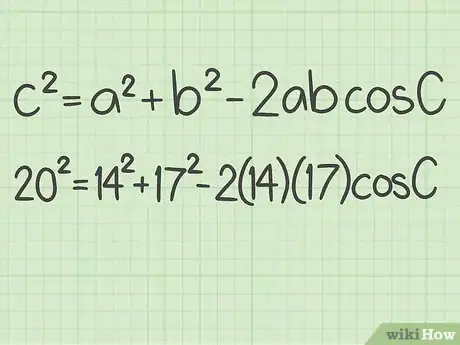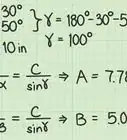How to Use the Laws of Sines and Cosines

Co-authored by wikiHow Staff

Last Updated: June 1, 2021 References

When you are missing side lengths or angle measurements of any triangle, you can use the law of sines, or the law of cosines, to help you find what you are looking for. The law of sines is ${\frac {a}{\sin {A}}}={\frac {b}{\sin {B}}}={\frac {c}{\sin {C}}}$ . The law of cosines is $c^{2}=a^{2}+b^{2}-2ab\cos {C}$ . In each formula $a$ , $b$ , and $c$ are the side lengths of the triangle. The angle opposite each side has a corresponding uppercase variable. Depending on what information you know about your triangle, you can use these two laws to solve for missing information.

Method 1

Method 1 of 4:

Using the Law of Sines to Find a Missing Side Length

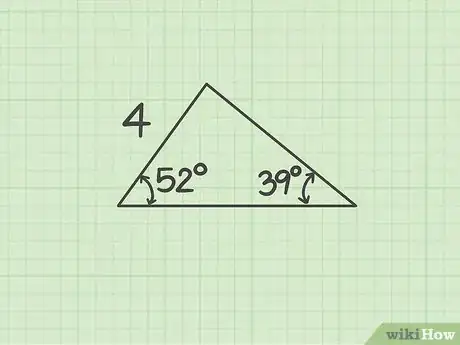
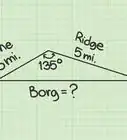
1
Assess what you know. To use the law of sines to find a missing side, you need to know at least two angles of the triangle and one side length.^{[1]
X
Research source}
- For example, you might have a triangle with two angles measuring 39 and 52 degrees, and you know that the side opposite the 39 degree angle is 4 cm long. You can use the law of sines to find both missing side lengths.
2
Identify and label sides and opposite angles. The convention is that side lengths are labeled $a$ $a$ , $b$ $b$ , and $c$ $c$ . The angle opposite each side is denoted by the capital letter of that side’s variable. For example, the angle opposite side $a$ $a$ is $A$ $A$ , the angle opposite side $b$ $b$ is $B$ $B$ , and the angle opposite side $c$ $c$ is $C$ $C$ .^{[2]
X
Research source}
- For example, in your triangle:
  $a=4cm$ ; $A=39\;{\text{degrees}}$
  $b=?$ ; $B=52\;{\text{degrees}}$
  $c=?$ ; $C=?$
Advertisement
3
Find the missing angle. The sum of all angles in a triangle is 180 degrees.^{[3]
X
Research source} Thus, if you know two angles of a triangle, you can find the third angle by subtracting both angles from 180.
- For example, since $A=39\;{\text{degrees}}$ and $B=52\;{\text{degrees}}$ , $C=180-39-52=89\;{\text{degrees}}$ .
4
Set up the formula for the law of sines. The formula is ${\frac {a}{\sin {A}}}={\frac {b}{\sin {B}}}={\frac {c}{\sin {C}}}$ . The formula shows that the ratio of one side of the triangle to the sine of the opposite angle is equal to the ratio of all other sides to their opposite angles.^{[4]
X
Research source}
5
Plug all the known values into the formula. Make sure you substitute side lengths for the lowercase variables, and angles for the capital variables. Also, remember that opposite sides and angles should have the same letter.
- For example, ${\frac {4}{\sin {39}}}={\frac {b}{\sin {52}}}={\frac {c}{\sin {89}}}$ .
6
Use a calculator to find the sines of the angles. You can also use a trigonometry table.^{[5]
X
Research source} Substitute the sines in the denominators of the ratios.
- For example, $\sin {39}=0.6293$ , $\sin {52}=0.788$ , and $\sin {89}=0.9998$ . So, your ratios will now look like this: ${\frac {4}{0.6293}}={\frac {b}{0.788}}={\frac {c}{0.9998}}$ .
7
Simplify the complete ratio. You have one complete ratio, with an angle and side. To simplify it, divide the numerator by the denominator.
- For example, ${\frac {4}{0.6293}}=6.3562$ .
8
Set the incomplete ratios equal to the complete ratio. To solve for a missing variable, multiply the complete ratio by the denominator of either incomplete ratio.
- For example:
  $6.3562={\frac {b}{0.788}}$
  $(6.3562)(0.788)=({\frac {b}{0.788}})(0.788)$
  $5.0087=b$
  
  AND
  
  $6.3562={\frac {c}{0.9998}}$
  $(6.3562)(0.9998)=({\frac {c}{0.9998}})(0.9998)$
  $6.3549=c$
  Thus, side $b$ is about 5 cm long, and side $c$ is about 6.35 cm long.

Method 2

Method 2 of 4:

Using the Law of Sines to Find a Missing Angle

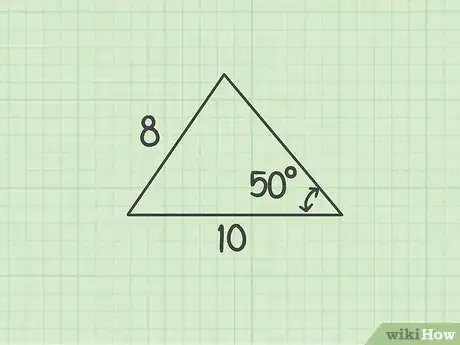
1
Assess what you know. To use the law of sines to find a missing angle, you need to know at least two side lengths and one angle.^{[6]
X
Research source}
- For example, you might have a triangle that has one side that is 10 cm long. Another side is 8 cm long, and the angle opposite is 50 degrees. You need to find the angle opposite the side that is 10 cm long.
2
Identify and label sides and opposite angles. The convention is that side lengths are labeled $a$ $a$ , $b$ $b$ , and $c$ $c$ . The angle opposite each side is denoted by the capital letter of that side’s variable. For example, the angle opposite side $a$ $a$ is $A$ $A$ , the angle opposite side $b$ $b$ is $B$ $B$ , and the angle opposite side $c$ $c$ is $C$ $C$ .^{[7]
X
Research source}
- For example, in your triangle:
  $a=8cm$ $a=8cm$ ; $A=50\;{\text{degrees}}$ $A=50\;{\text{degrees}}$
  $b=10cm$ $b=10cm$ ; $B=?$ $B=?$
  $c=?$ $c=?$ ; $C=?$ $C=?$
  - Since you want to find the angle opposite the 10 cm side, you are looking for angle B.
3
Set up the formula for the law of sines. The formula is ${\frac {a}{\sin {A}}}={\frac {b}{\sin {B}}}={\frac {c}{\sin {C}}}$ . The formula shows that the ratio of one side of the triangle to the sine of the opposite angle is equal to the ratio of all other sides to their opposite angles.^{[8]
X
Research source}
4
Plug all the known values into the formula. Take care to substitute the values correctly, so that the side lengths are in the numerators of the formula, and their opposite angles are in the corresponding denominators.
- For example, ${\frac {8}{\sin {50}}}={\frac {10}{\sin {B}}}={\frac {c}{\sin {C}}}$ .
5
Set up an equation to find the missing angle. To do this, set the complete ratio equal to the ratio with the angle you are solving for. Take the reciprocal of each ratio, so that the side length is in the denominator, and the sine of the angle is in the numerator.^{[9]
X
Research source}
- For example, since you know side $a$ and angle $A$ , and are solving for angle $B$ , you would set up the ratio ${\frac {8}{\sin {50}}}={\frac {10}{\sin {B}}}$ . Taking the reciprocals, you have ${\frac {\sin {50}}{8}}={\frac {\sin {B}}{10}}$ .
6
Find the sine of the known angle. Use a calculator or trigonometry table to do this. Plug the decimal into the equation.
- For example, $\sin {50}=0.766$ . So, the equation should now look like this: ${\frac {0.766}{8}}={\frac {\sin {B}}{10}}$
7
Isolate the missing sine and simplify the equation. To do this, multiply each side of the equation by the unknown angle’s denominator, then simplify the remaining ratio.
- For example:
  ${\frac {\sin {50}}{8}}={\frac {\sin {B}}{10}}$
  $({\frac {0.766}{8}})(10)=({\frac {\sin {B}}{10}})(10)$
  ${\frac {0.766\times 10}{8}}=\sin {B}$
  ${\frac {7.66}{8}}=\sin {B}$
  $0.9575=\sin {B}$
8
Find the inverse sine. The inverse sine is shown by the $SIN^{-1}$ $SIN^{{-1}}$ button on a calculator. The inverse sine will give you measurement of the missing angle.^{[10]
X
Research source}
- For example, the inverse sine of 0.9575 is 73.2358. So, angle $B$ is about 73.24 degrees.

Method 3

Method 3 of 4:

Using the Law of Cosines to Find a Missing Side Length

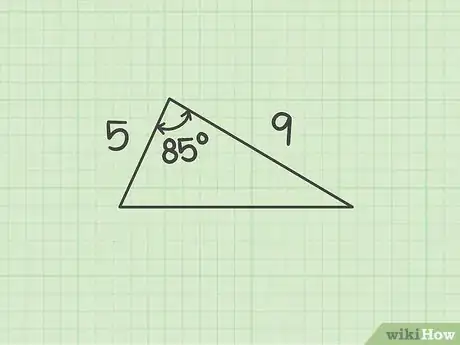
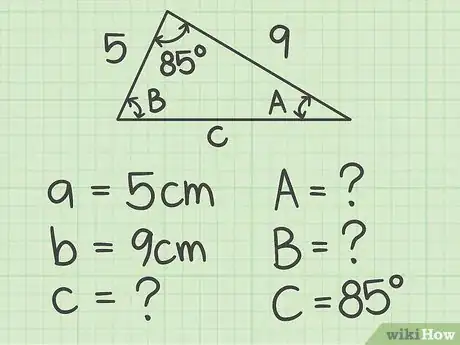
1
Assess what you know. To find a missing side length using the law of cosines, you need to know the length of the other two sides of the triangles, and the measurement of the angle between them.^{[11]
X
Research source}
- For example, you might have a triangle with sides that are 5 and 9 cm long, and the angle between them is 85 degrees. You need to find the length of the missing side.
2
Identify and label sides and opposite angles. The convention is that side lengths are labeled $a$ $a$ , $b$ $b$ , and $c$ $c$ . The angle opposite each side is denoted by the capital letter of that side’s variable. For example, the angle opposite side $a$ $a$ is $A$ $A$ , the angle opposite side $b$ $b$ is $B$ $B$ , and the angle opposite side $c$ $c$ is $C$ $C$ .^{[12]
X
Research source}
- For example, in your triangle:
  $a=5cm$ $a=5cm$ ; $A=?$ $A=?$
  $b=9cm$ $b=9cm$ ; $B=?$ $B=?$
  $c=?$ $c=?$ ; $C=85$ $C=85$
  - Since you want to find the side opposite the 85 degree angle, you are looking for side $c$ .
3
Set up the formula for the law of cosines. The formula is $c^{2}=a^{2}+b^{2}-2ab\cos {C}$ . In this formula, $c$ is the missing side length.^{[13]
X
Research source}
4
Plug all the known values into the formula. Make sure you substitute the correct values for the correct variables. The side you are trying to find should be $c$ $c$ , and the angle you know should be $C$ $C$ .
- For example, $c^{2}=5^{2}+9^{2}-2(5)(9)\cos {85}$ .
5
Use a calculator to find the cosine of the angle. Plug this value into the equation, and multiply.
- For example, $\cos {85}=0.0872$ . So, your equation should now look like this: $c^{2}=5^{2}+9^{2}-2(5)(9)(0.0872)$ .
  Multiplying, you get $c^{2}=5^{2}+9^{2}-7.844$ .
6
Square the known side lengths. Remember that to square a number means to multiply the number by itself. Square the numbers, then add them together.
- For example:
  $c^{2}=25+81-7.844$
  $c^{2}=106-7.844$
7
Find the difference. This will give you the value of $c^{2}$ $c^{{2}}$ . Then, you can take the square root of both sides of the equation to find $c$ $c$ .^{[14]
X
Research source}
- For example:
  $c^{2}=106-7.844$
  $c^{2}=98.156$
  ${\sqrt {c^{2}}}={\sqrt {98.156}}$
  $c=9.9074$
  Thus, side $c$ is about 9.91 cm long.

Method 4

Method 4 of 4:

Using Law of Cosines to Find a Missing Angle

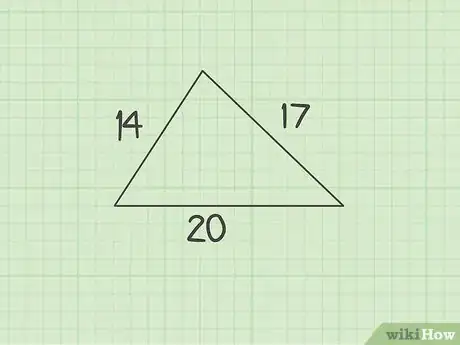
1
Assess what you know. To find the missing angle using the law of cosines, you need to know the length of all three sides of the triangle.^{[15]
X
Research source}
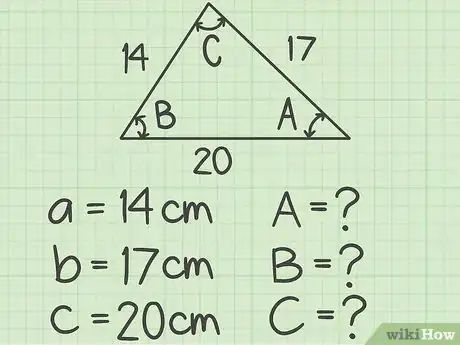
- For example, you might have a triangle with sides measuring 14, 17, and 20 cm. You need to find the angle opposite the 20 cm side.
2
Identify and label sides and opposite angles. The convention is that side lengths are labeled $a$ $a$ , $b$ $b$ , and $c$ $c$ . The angle opposite each side is denoted by the capital letter of that side’s variable. For example, the angle opposite side $a$ $a$ is $A$ $A$ , the angle opposite side $b$ $b$ is $B$ $B$ , and the angle opposite side $c$ $c$ is $C$ $C$ .^{[16]
X
Research source}
- For example, in your triangle:
  $a=14cm$ $a=14cm$ ; $A=?$ $A=?$
  $b=17cm$ $b=17cm$ ; $B=?$ $B=?$
  $c=20cm$ $c=20cm$ ; $C=?$ $C=?$
  - Since you want to find the side opposite the 20 cm side, you are looking for side $c$ .
3
Set up the formula for the law of cosines. The formula is $c^{2}=a^{2}+b^{2}-2ab\cos {C}$ . In this formula, $C$ is the angle you are trying to find.^{[17]
X
Research source}
4
Plug all the known values into the formula. Make sure you substitute the correct values for the correct variables. The angle you are trying to find should be $C$ $C$ . This means that $c$ $c$ should be the side opposite the angle you are trying to solve.
- For example, $20^{2}=14^{2}+17^{2}-2(14)(17)\cos {C}$ .
5
Simplify the expression using the order of operations. First, find the squares of the side lengths. Then, make the appropriate multiplications. Then, add.
- For example:
  $20^{2}=14^{2}+17^{2}-2(14)(17)\cos {C}$
  $400=196+289-2(14)(17)\cos {C}$
  $400=196+289-(476)\cos {C}$
  $400=485-(476)\cos {C}$
6
Isolate the cosine. To do this, subtract the sum of the squares of sides $a$ $a$ and $b$ $b$ from each side of the equation. Then, divide each side by the cosine’s coefficient.
- For example:
  $400=485-(476)\cos {C}$
  $400-485=485-485-(476)\cos {C}$
  $-85=(-476)\cos {C}$
  ${\frac {-85}{-476}}={\frac {(-476)\cos {C}}{-476}}$
  $0.1786=\cos {C}$
7
Find the inverse cosine. Use the $COS^{-1}$ $COS^{{-1}}$ key on a calculator to do this. The inverse cosine will give you the measurement of the missing angle.^{[18]
X
Research source}
- For example, the inverse cosine of 0.1786 is 79.7134. So, angle $C$ is about 79.71 degrees.