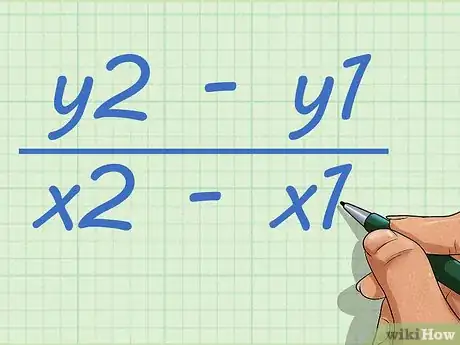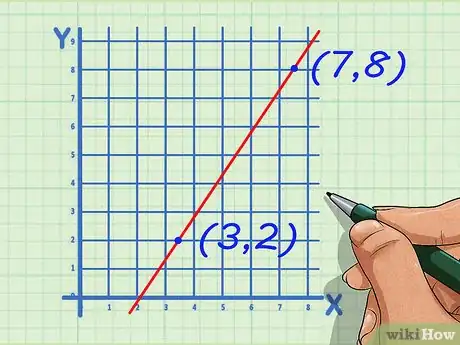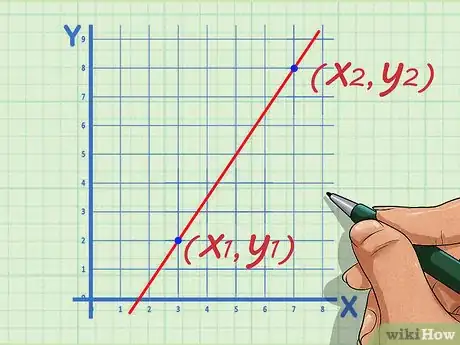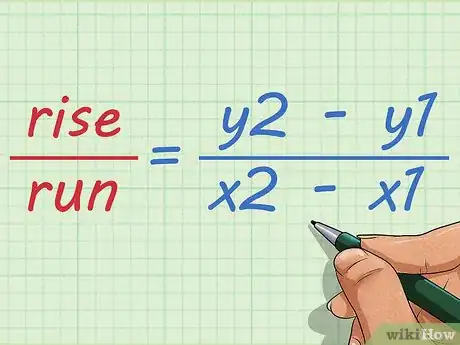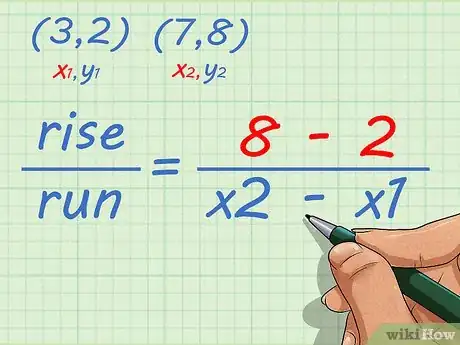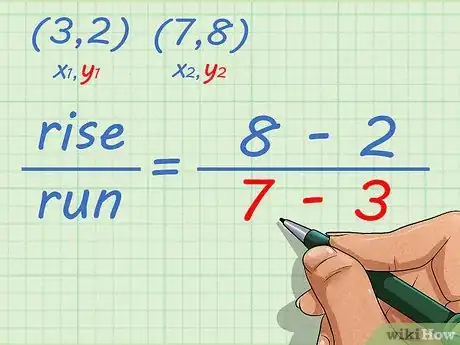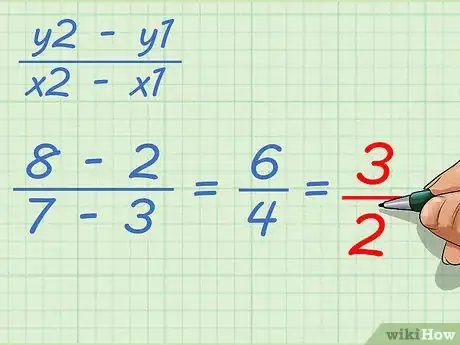This article was co-authored by wikiHow Staff. Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow's Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards.
This article has been viewed 76,064 times.
Learn more...
Finding the slope of a line is an essential skill in coordinate geometry, and is often used to draw a line on graph, or to determine the x- and y-intercepts of a line. The slope of a line is a measure of how steep the line is,[1] which is found be determining how many units the line moves vertically per how many units it moves horizontally. You can easily calculate the slope of a line using the coordinates of two of its points.
Steps
Practice Problems
Setting up the Problem
-
1Understand the slope formula. Slope is defined as “rise over run,” with rise indicating vertical distance between two points, and run indicating the horizontal distance between two points.[2]
-
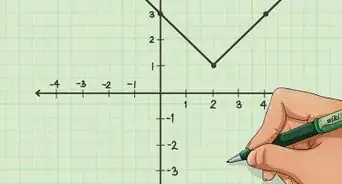
2Pick two points on the line and label their coordinates. These can be any points the line runs through.
- You can also use this method if you are given two points on the line, without having the line graphed in front of you.
- Coordinates are listed as , with being the location along the x, or horizontal axis, and being the location along the y, or vertical axis.
- For example, you might choose points with coordinates and .
Advertisement -
3Determine the order of your points. One point will be point 1, and one point will be point 2. It doesn’t matter which point is which, as long as you keep them in the correct order throughout the calculation.[3]
- The first point’s coordinates will be , and the second point’s coordinates will be
-
4Set up the slope formula. The formula is . The change in y-coordinates determines the rise, and the change in x-coordinates determines the run.[4]
Finding the Rise and Run
-
1Plug the y-coordinates into the slope formula. Make sure you are not using the x-coordinates, and that you are substituting the correct y-coordinates for the first and second points.[5]
- For example, if the coordinates of your first point are , and the coordinates of your second point are , your formula will look like this:
- For example, if the coordinates of your first point are , and the coordinates of your second point are , your formula will look like this:
-
2Plug the x-coordinates into the slope formula. Make sure you are not using the y-coordinates, and that you are substituting the correct x-coordinates for the first and second points.[6]
- For example, if the coordinates of your first point are , and the coordinates of your second point are , your formula will look like this:
- For example, if the coordinates of your first point are , and the coordinates of your second point are , your formula will look like this:
-
3Subtract the y-coordinates. This will give you your rise.[7]
- For example, if your y-coordinates are and , you would calculate .
-
4Subtract the x-coordinates. This will give you your run.[8]
- For example, if your x-coordinates are and , you would calculate .
-
5Reduce the fraction if necessary. This result will give you the slope of your line.[9]
- For complete instructions on how to reduce a fraction, read Reduce Fractions.
- For example, can be reduced to , so the slope of a line through points and is .
-
6Be careful when working with negative numbers. A slope can be positive or negative. A line with a positive slope moves up left-to-right; a line with a negative slope moves down left-to-right.
- Remember, if the numerator and denominator are both negative, then the negative signs cancel out, and the fraction (and slope) is positive.
- If either the numerator or the denominator is negative, then the fraction (and slope) is negative.
-
7Check your work. To do this, look at the rise and run you calculated for your slope. Starting at your first point, count up the rise, then over the run. Repeat counting up the rise and over the run until you reach your second point.
- If you do not reach your second point, then your calculation is incorrect.
Community Q&A
-
QuestionWhat does a negative slope look like?
 Community AnswerA negative slope moves down, left-to-right.
Community AnswerA negative slope moves down, left-to-right. -
QuestionCan you do this without a graph, like when they give you 2 coordinates?
 Emma HanCommunity AnswerYes you can. The graph is only there to help you. You can only find the gradient if they give you 2 points.
Emma HanCommunity AnswerYes you can. The graph is only there to help you. You can only find the gradient if they give you 2 points. -
QuestionHow do you compute slope with (-6,3) and (2,9)?
 GB742Top AnswererUse the formula m = (y2 - y1)/(x2 - x1). In this example: (9 - 3)/(2 - -6) = (6)/(8). Therefore, the slope of the line connecting (-6,3) and (2,9) is 6/8.
GB742Top AnswererUse the formula m = (y2 - y1)/(x2 - x1). In this example: (9 - 3)/(2 - -6) = (6)/(8). Therefore, the slope of the line connecting (-6,3) and (2,9) is 6/8.
References
- ↑ http://www.mathopenref.com/coordslope.html
- ↑ https://www.khanacademy.org/math/cc-eighth-grade-math/cc-8th-linear-equations-functions/8th-slope/a/slope-formula
- ↑ http://www.purplemath.com/modules/slope.htm
- ↑ http://www.coolmath.com/algebra/08-lines/06-finding-slope-line-given-two-points-01
- ↑ https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:linear-equations-graphs/x2f8bb11595b61c86:slope/a/slope-review
- ↑ https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:linear-equations-graphs/x2f8bb11595b61c86:slope/a/slope-review
- ↑ https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:linear-equations-graphs/x2f8bb11595b61c86:slope/a/slope-review
- ↑ https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:linear-equations-graphs/x2f8bb11595b61c86:slope/a/slope-review
- ↑ https://courses.lumenlearning.com/suny-beginalgebra/chapter/read-or-watch-find-slope-from-a-graph/