wikiHow is a “wiki,” similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, 41 people, some anonymous, worked to edit and improve it over time.
There are 8 references cited in this article, which can be found at the bottom of the page.
This article has been viewed 440,673 times.
Learn more...
The distance to the horizon depends almost completely on the height above sea-level that the observer is looking from. Knowing this number is extremely useful and often necessary when navigating over the ocean or going on a hike, though just being curious is reason enough! There are also a few other factors that you might have to consider depending on where you are in the world and the time at which you are viewing, such as temperature and weather conditions. Once you have all the measures you need, you can quickly get the calculation and know the exact distance you are from the horizon.
Steps
Calculating Distance Using Geometry
-
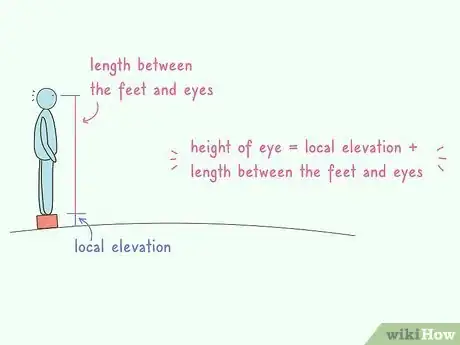
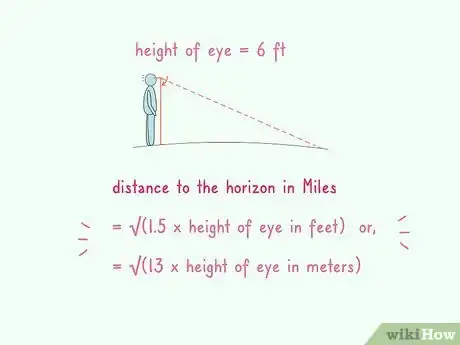
1Measure your "height of eye." Measure the length between the ground and your eyes in meters or feet. One way to calculate this is to measure the distance between your eyes and the top of your head. Subtract this value from your total height and what will be left is the distance between your eyes and the surface you're standing on. If you are standing exactly at sea level, with the bottom of your feet level with the water, this is the only measurement you'll need.[1]
-
2Add your "local elevation" if you're standing on a raised surface, such as a hill, building or boat. How many meters or feet above the true horizon are you standing? 1 meter? 4,000 feet? Add that number to your height of eye (in the same units, of course).[2]Advertisement
-
3Multiply by 13m if you took the measurement in meters, or multiply by 1.5ft if you took the measurement in feet.
-
4Take the square root to find the answer.[3] If you used meters, your answer will be in kilometers, and if feet, the answer will be in miles. The distance calculated is a straight line from your eyes to the horizon.
- The actual distance you'll travel to get to the horizon will be longer because of surface curvature and (on land) irregularities. Proceed to the next method below for a more accurate (but complicated) formula.
-
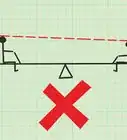
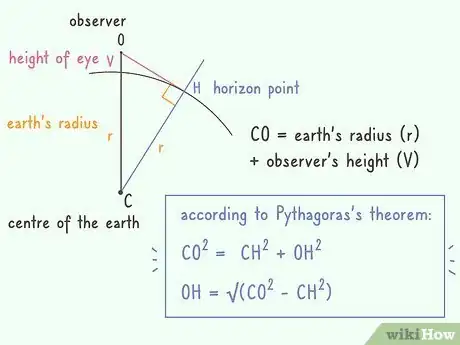
5Understand how this calculation works. It's based on a triangle formed by your observation point (your eyes), the true horizon point (what you're looking at) and the center of the Earth.[4]
- By knowing the radius of the Earth and measuring your height of eye and local elevation, that leaves only the distance between your eyes and the horizon as unknown. Since the sides of the triangle that meet at the horizon actually form a right angle, we can use the Pythagorean theorem (good old a2 + b2 = c2) as the basis for this calculation, where:
• a = R (the radius of the Earth)
• b = the distance to the horizon, unknown
• c = h (your height of eye) + R
- By knowing the radius of the Earth and measuring your height of eye and local elevation, that leaves only the distance between your eyes and the horizon as unknown. Since the sides of the triangle that meet at the horizon actually form a right angle, we can use the Pythagorean theorem (good old a2 + b2 = c2) as the basis for this calculation, where:
Calculating Distance Using Trigonometry
-
1Calculate the actual distance you'd have to traverse to get to the horizon by using the following formula.
- d = R * arccos(R/(R + h)), where
• d = distance to horizon
• R = radius of the Earth
• h = height of eye
- d = R * arccos(R/(R + h)), where
-
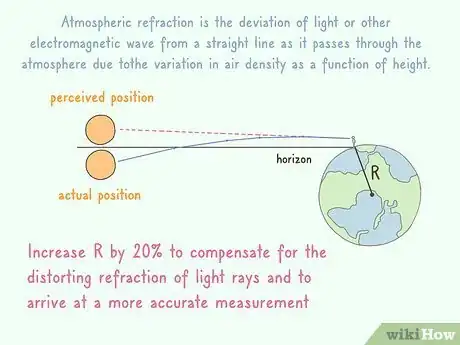
2Increase R by 20% to compensate for the distorting refraction of light rays and to arrive at a more accurate measurement. The geometric horizon calculated using the method in this article may not be the same as the optical horizon, which is what your eye actually sees. Why is this?[5]
- The atmosphere bends (refracts) light that is traveling horizontally. What this usually means is that a ray of light is able to slightly follow the curvature of the earth, so that the optical horizon is a bit further away than the geometric horizon.
- Unfortunately the refraction due to the atmosphere is neither constant nor predictable, as it depends on the change of temperature with height. There is therefore no simple way to add a correction to the formula for the geometric horizon, though one may achieve an "average" correction by assuming a radius for the earth that is a bit greater than the true radius.
-
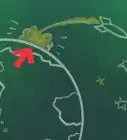
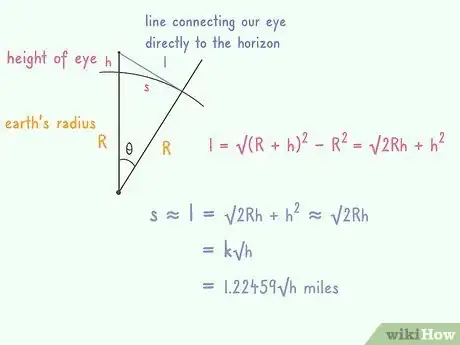
3Understand how this calculation works. This will calculate the length of the curved line that follows from your feet to the true horizon (shown in green in this image). Now, the arccos(R/(R+h)) portion refers to the angle that is made at the center of the Earth by the line going from the true horizon to the center and the line going from you to the center. With this angle, we multiply it by R to get the "arc length," which, in this case, is the distance that you are looking for.[6]
Alternate Geometrical Calculation
-
1Assume a flat plane or the ocean. This method is a simpler version of the first set of instructions presented in this article, and applies only in feet and miles.
-
2Solve for the distance in miles by plugging in your height of eye in feet (h) into the formula. The formula you will be using is d = 1.2246* SQRT(h).[7]
-
3
Community Q&A
-
QuestionCan I see an object beyond the horizon?
 Community AnswerNot the entire object, but you might be able to see part of it if it's tall enough. If something like a tree or a building is standing just beyond the horizon, you might be able to see the upper part of it.
Community AnswerNot the entire object, but you might be able to see part of it if it's tall enough. If something like a tree or a building is standing just beyond the horizon, you might be able to see the upper part of it. -
QuestionWhy wouldn't the formula for determining distance to the horizon work in a city or a forest?
 Community AnswerThe trees in the forest or the buildings in the city would affect the view.
Community AnswerThe trees in the forest or the buildings in the city would affect the view. -
QuestionHow many acres in 630 sq ft?
 DonaganTop AnswererBecause there are 43,560 square feet in an acre, 630 square feet equal 630 / 43,560 = 0.01446 acre.
DonaganTop AnswererBecause there are 43,560 square feet in an acre, 630 square feet equal 630 / 43,560 = 0.01446 acre.
References
- ↑ http://www.fao.org/fishery/static/FAO_Training/FAO_Training/General/x6707e/x6707e04.htm
- ↑ http://www.fao.org/fishery/static/FAO_Training/FAO_Training/General/x6707e/x6707e04.htm
- ↑ https://www.cuemath.com/algebra/squares-and-square-roots/
- ↑ https://aty.sdsu.edu/explain/atmos_refr/horizon.html
- ↑ https://www.nwcg.gov/course/ffm/vert-horiz-and-slope/45-slope
- ↑ https://sites.math.washington.edu/~conroy/m120-general/horizon.pdf
- ↑ https://aty.sdsu.edu/explain/atmos_refr/horizon.html
- ↑ https://www.mathalino.com/reviewer/derivation-of-formulas/derivation-of-pythagorean-theorem
- ↑ https://aty.sdsu.edu/explain/atmos_refr/horizon.html
About This Article
Before calculating distance to the horizon if you’re standing exactly at sea level, start by measuring your total height, unless you already know it. Once you’ve got your height, measure the distance between the ground and your eyes. Then, subtract the distance measurement from your total height. The amount remaining is the distance between your eyes and the surface you’re standing on. Multiply by 13 meters if you took the measurement in meters, or multiply by 1.5 feet if you took the measurement in feet. Take the square root to get your answer, which will be in kilometers if you measured in meters or in miles if you measured in feet. Your calculated distance is a straight line from your eyes to the horizon. For more tips, including how to measure from an elevated point, read on.




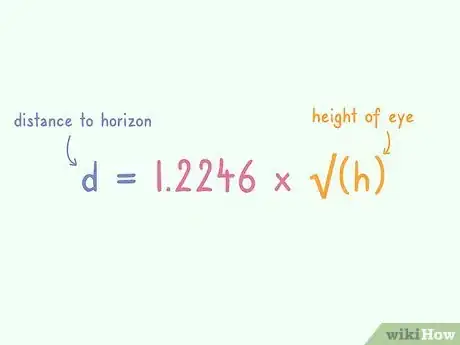





-Step-8-Version-2.webp)