In statistics, simple linear regression is the least squares estimator of a linear regression model with a single explanatory variable. Simple linear regression fits a straight line through the set of
The slope of the fitted line is equal to the correlation between
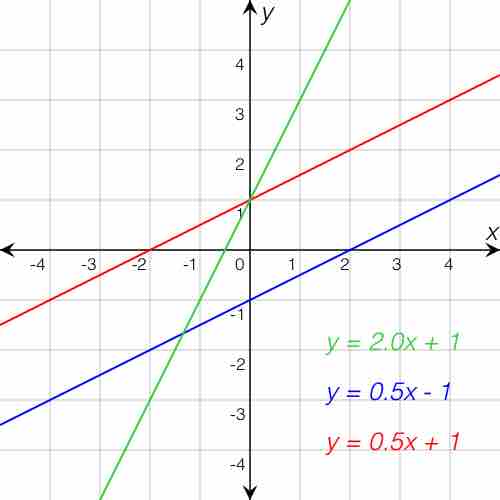
The function of a lne
Three lines — the red and blue lines have the same slope, while the red and green ones have same y-intercept.
Linear regression was the first type of regression analysis to be studied rigorously, and to be used extensively in practical applications. This is because models which depend linearly on their unknown parameters are easier to fit than models which are non-linearly related to their parameters and because the statistical properties of the resulting estimators are easier to determine.
A common form of a linear equation in the two variables
Where
If the goal is prediction, or forecasting, linear regression can be used to fit a predictive model to an observed data set of
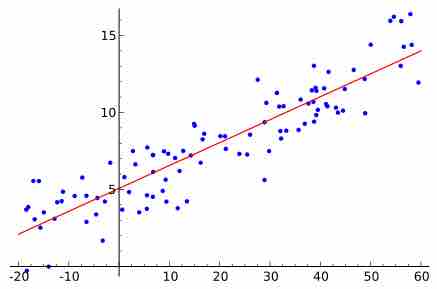
Linear regression
An example of a simple linear regression analysis