Interaction Models

In statistics, an interaction may arise when considering the relationship among three or more variables, and describes a situation in which the simultaneous influence of two variables on a third is not additive. Most commonly, interactions are considered in the context of regression analyses.

The presence of interactions can have important implications for the interpretation of statistical models. If two variables of interest interact, the relationship between each of the interacting variables and a third "dependent variable" depends on the value of the other interacting variable. In practice, this makes it more difficult to predict the consequences of changing the value of a variable, particularly if the variables it interacts with are hard to measure or difficult to control.

The notion of "interaction" is closely related to that of "moderation" that is common in social and health science research: the interaction between an explanatory variable and an environmental variable suggests that the effect of the explanatory variable has been moderated or modified by the environmental variable.

Interaction Variables in Modeling

An interaction variable is a variable constructed from an original set of variables in order to represent either all of the interaction present or some part of it. In exploratory statistical analyses, it is common to use products of original variables as the basis of testing whether interaction is present with the possibility of substituting other more realistic interaction variables at a later stage. When there are more than two explanatory variables, several interaction variables are constructed, with pairwise-products representing pairwise-interactions and higher order products representing higher order interactions.

A simple setting in which interactions can arise is a two-factor experiment analyzed using Analysis of Variance (ANOVA). Suppose we have two binary factors $A$ and $B$. For example, these factors might indicate whether either of two treatments were administered to a patient, with the treatments applied either singly, or in combination. We can then consider the average treatment response (e.g. the symptom levels following treatment) for each patient, as a function of the treatment combination that was administered. The following table shows one possible situation:

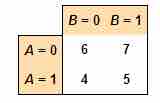
Interaction Model 1

A table showing no interaction between the two treatments — their effects are additive.

In this example, there is no interaction between the two treatments — their effects are additive. The reason for this is that the difference in mean response between those subjects receiving treatment $A$ and those not receiving treatment $A$ is $-2$, regardless of whether treatment $B$ is administered ($-2 = 4-6$) or not ($-2 = 5-7$). Note: It automatically follows that the difference in mean response between those subjects receiving treatment $B$ and those not receiving treatment $B$ is the same, regardless of whether treatment $A$ is administered ($7=6=5-4$).

In contrast, if the average responses as in are observed, then there is an interaction between the treatments — their effects are not additive. Supposing that greater numbers correspond to a better response, in this situation treatment $B$ is helpful on average if the subject is not also receiving treatment $A$, but is more helpful on average if given in combination with treatment $A$. Treatment $A$ is helpful on average regardless of whether treatment $B$ is also administered, but it is more helpful in both absolute and relative terms if given alone, rather than in combination with treatment $B$.

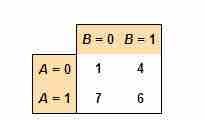
Interaction Model 2

A table showing an interaction between the treatments — their effects are not additive.