Polynomial Regression
Polynomial regression is a higher order form of linear regression in which the relationship between the independent variable
History
Polynomial regression models are usually fit using the method of least-squares. The least-squares method minimizes the variance of the unbiased estimators of the coefficients, under the conditions of the Gauss–Markov theorem. The least-squares method was published in 1805 by Legendre and in 1809 by Gauss. The first design of an experiment for polynomial regression appeared in an 1815 paper of Gergonne. In the 20th century, polynomial regression played an important role in the development of regression analysis, with a greater emphasis on issues of design and inference. More recently, the use of polynomial models has been complemented by other methods, with non-polynomial models having advantages for some classes of problems.
Interpretation
Although polynomial regression is technically a special case of multiple linear regression, the interpretation of a fitted polynomial regression model requires a somewhat different perspective. It is often difficult to interpret the individual coefficients in a polynomial regression fit, since the underlying monomials can be highly correlated. For example,
Alternative Approaches
Polynomial regression is one example of regression analysis using basis functions to model a functional relationship between two quantities. A drawback of polynomial bases is that the basis functions are "non-local," meaning that the fitted value of
The goal of polynomial regression is to model a non-linear relationship between the independent and dependent variables (technically, between the independent variable and the conditional mean of the dependent variable). This is similar to the goal of non-parametric regression, which aims to capture non-linear regression relationships. Therefore, non-parametric regression approaches such as smoothing can be useful alternatives to polynomial regression. Some of these methods make use of a localized form of classical polynomial regression. An advantage of traditional polynomial regression is that the inferential framework of multiple regression can be used.
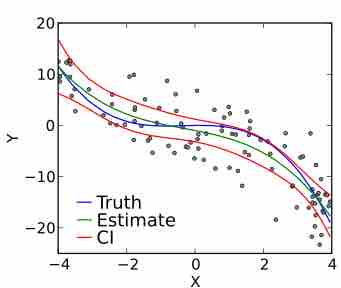
Polynomial Regression
A cubic polynomial regression fit to a simulated data set.