Chapter 27
Special Relativity
By Boundless
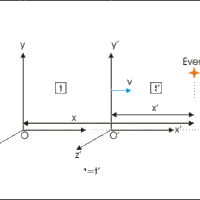
Galilean invariance or Galilean relativity states that the laws of motion are the same in all inertial (or non-accelerating) frames.

Special relativity is based on Einstein's two postulates: the Principle of Relativity and the Principle of Invariant Light Speed.
The speed of light in vacuum is a universal physical constant crucial to many areas of physics.
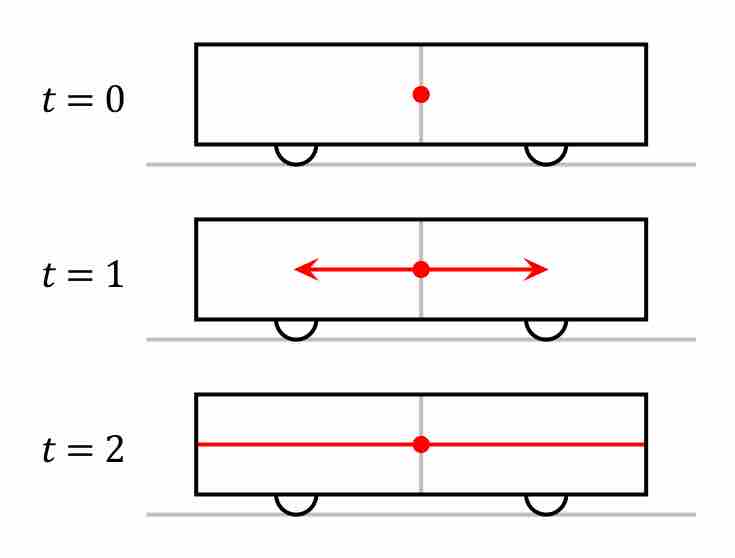
The relativity of simultaneity is the concept that simultaneity is not absolute, but depends on the observer's reference frame.

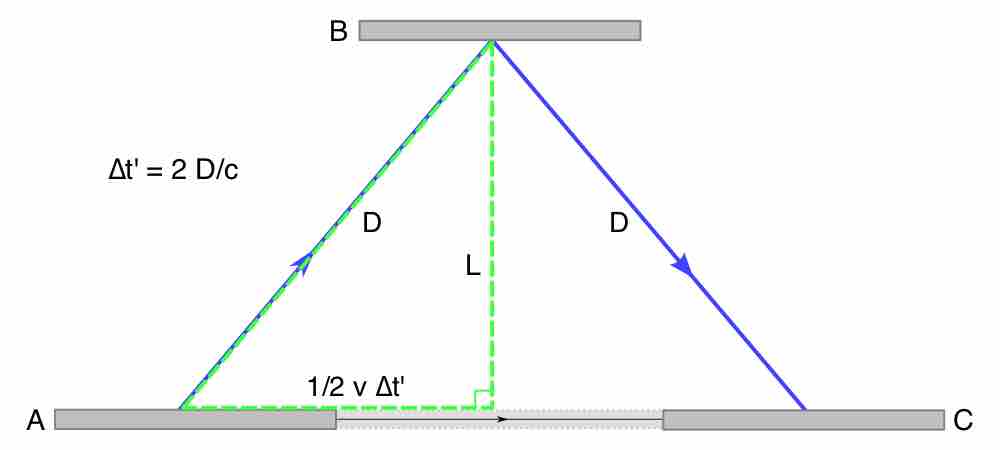
Time dilation is an actual difference of elapsed time between two events as measured by observers moving relative to each other.
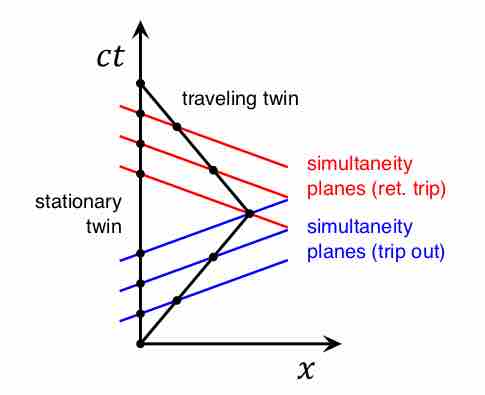
The twin paradox is a thought experiment: one twin makes a journey into space and returns home to find that twin remained aged more.
Objects that are moving undergo a length contraction along the dimension of motion; this effect is only significant at relativistic speeds.
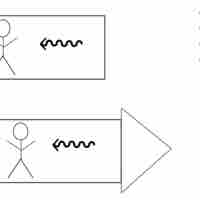
A velocity-addition formula is an equation that relates the velocities of moving objects in different reference frames.

Relativistic momentum is given as

In special relativity, as the object approaches the speed of light, the object's energy and momentum increase without bound.

Antimatter is composed of antiparticles, which have the same mass as particles of ordinary matter but opposite charge and quantum spin.

Relativistic kinetic energy can be expressed as:
Special relativity changed the way we view space and time and showed us that time is relative to an observer.
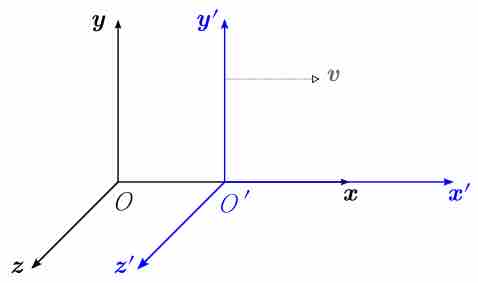
We live in four-dimensional space-time, in which the ordering of certain events can depend on the observer.
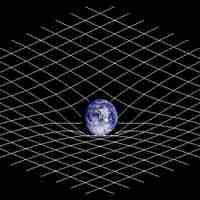
Gravity is a geometrical effect in which a metric matrix plays a special role, and the motion of objects are altered by curved space.