Relativistic Energy and Mass

Relativistic Energy and Mass

In special relativity, an object that has a mass cannot travel at the speed of light. As the object approaches the speed of light, the object's energy and momentum increase without bound . Relativistic corrections for energy and mass need to be made because of the fact that the speed of light in a vacuum is constant in all reference frames. The conservation of mass and energy are well-accepted laws of physics. In order for these laws to hold in all reference frames, special relativity must be applied. It is important to note that for objects with speeds that are well below the speed of light that the expressions for relativistic energy and mass yield values that are approximately equal to their Newtonian counterparts.

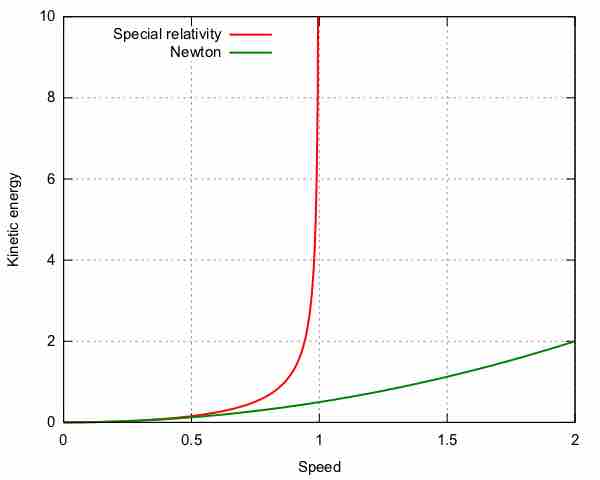
Relativistic and Newtonian Kinetic Energy

This figure illustrates how relativistic and Newtonian Kinetic Energy are related to the speed of an object. The relativistic kinetic energy increases to infinity when an object approaches the speed of light, this indicates that no body with mass can reach the speed of light. On the other hand, Newtonian kinetic energy continues to increase without bound as the speed of an object increases.

Relativistic Mass

Relativistic mass was defined by Richard C. Tolman pictured left of Albert Einstein here in 1934 as which holds for all particles, including those moving at the speed of light. For a slower than light particle, a particle with a nonzero rest mass, the formula becomes where is the rest mass and is the Lorentz factor. The Lorentz factor is equal to: $\gamma = \frac{1}{\sqrt{1 - v^2/c^2}}$, where v is the relative velocity between inertial reference frames and c is the speed of light.

Richard C. Tolman and Albert Einstein

Richard C. Tolman (1881 - 1948) with Albert Einstein (1879 - 1955) at Caltech, 1932

When the relative velocity is zero, is simply equal to 1, and the relativistic mass is reduced to the rest mass. As the velocity increases toward the speed of light (c), the denominator of the right side approaches zero, and consequently approaches infinity.

In the formula for momentum the mass that occurs is the relativistic mass. In other words, the relativistic mass is the proportionality constant between the velocity and the momentum.

While Newton's second law remains valid in the form the derived form is not valid because in is generally not a constant.

Relativistic Energy

Relativistic energy ($E_{r} = \sqrt{(m_{0}c^{2})^{2} + (pc)^{^{2}}}$) is connected with rest mass via the following equation: $m = \frac{\sqrt{(E^{2} - (pc)^{^{2}}}}{c^{2}}$. Here the term represents the square of the Euclidean norm (total vector length) of the various momentum vectors in the system, which reduces to the square of the simple momentum magnitude, if only a single particle is considered. This equation reduces to when the momentum term is zero. For photons where the equation reduces to .

Today, the predictions of relativistic energy and mass are routinely confirmed from the experimental data of particle accelerators such as the Relativistic Heavy Ion Collider. The increase of relativistic momentum and energy is not only precisely measured but also necessary to understand the behavior of cyclotrons and synchrotron, which accelerate particles to near the speed of light.