Angular Velocity, Omega

To examine how fast an object is rotating, we define angular velocity ω as the rate of change of an angle. In symbols, this is

$\omega = \Delta \theta/\Delta t$,

where an angular rotation Δ takes place in a time Δt. The greater the rotation angle in a given amount of time, the greater the angular velocity. The units for angular velocity are radians per second (rad/s).

Angular velocity ω is analogous to linear velocity v. To find the precise relationship between angular and linear velocity, we again consider a pit on the rotating CD. This pit moves an arc length Δs in a time Δt, and so it has a linear velocity v = Δs/Δt.

From $\Delta \theta = (\Delta s)/r$ we see that $\Delta s = r\cdot \Delta \theta$. Substituting this into the expression for v gives $v = (r\cdot\Delta \theta)/(\Delta t) = r(\Delta \theta/\Delta t) = r\omega$.

We can write this relationship in two different ways: v=rω or ω=v/r.

The first relationship states that the linear velocity v is proportional to the distance from the center of rotation, thus it is largest for a point on the rim (largest r), as you might expect. We can also call this linear speed v of a point on the rim the tangential speed. The second relationship can be illustrated by considering the tire of a moving car, as shown in the picture below. Note that the speed of the point at the center of the tire is the same as the speed v of the car. The faster the car moves, the faster the tire spins—large v means a large ω, because v=rω. Similarly, a larger-radius tire rotating at the same angular velocity (ω) will produce a greater linear speed (v) for the car.

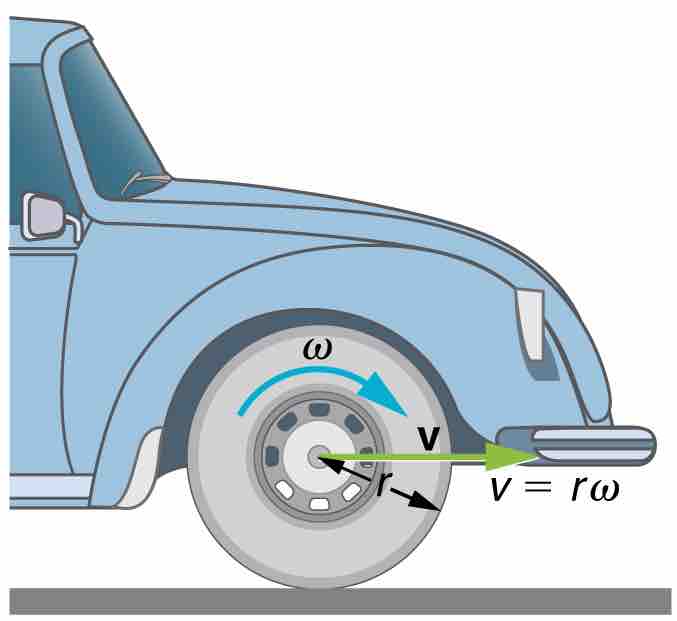
Angular Velocity

A car moving at a velocity v to the right has a tire rotating with an angular velocity ω. The speed of the tread of the tire relative to the axle is v, the same as if the car were jacked up. Thus the car moves forward at linear velocity v=rω, where r is the tire radius. A larger angular velocity for the tire means a greater velocity for the car.