Angular acceleration is the rate of change of angular velocity. In SI units, it is measured in radians per second squared (rad/s2), and is usually denoted by the Greek letter alpha (
Consider the following situations in which angular velocity is not constant: when a skater pulls in her arms, when a child starts up a merry-go-round from rest, or when a computer's hard disk slows to a halt when switched off. In all these cases, there is an angular acceleration in which
where
It is useful to know how linear and angular acceleration are related. In circular motion, there is acceleration that is tangent to the circle at the point of interest (as seen in the diagram below). This acceleration is called tangential acceleration, at.
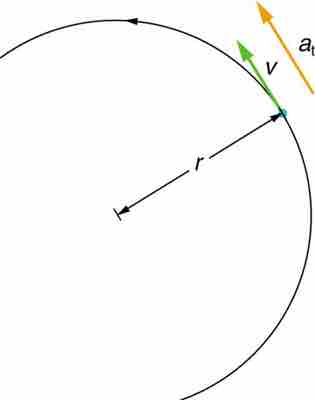
Tangential acceleration
In circular motion, acceleration can occur as the magnitude of the velocity changes: a is tangent to the motion. This acceleration is called tangential acceleration.
Tangential acceleration refers to changes in the magnitude of velocity but not its direction. In circular motion, centripetal acceleration, ac, refers to changes in the direction of the velocity but not its magnitude. An object undergoing circular motion experiences centripetal acceleration (as seen in the diagram below.) Thus, at and ac are perpendicular and independent of one another. Tangential acceleration at is directly related to the angular acceleration and is linked to an increase or decrease in the velocity (but not its direction).
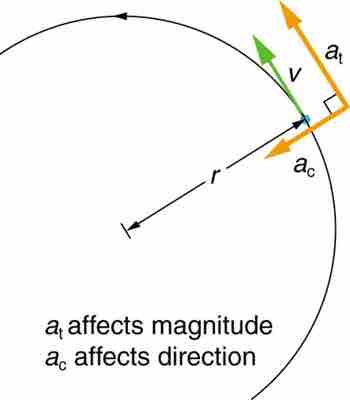
Centripetal Acceleration
Centripetal acceleration occurs as the direction of velocity changes; it is perpendicular to the circular motion. Centripetal and tangential acceleration are thus perpendicular to each other.