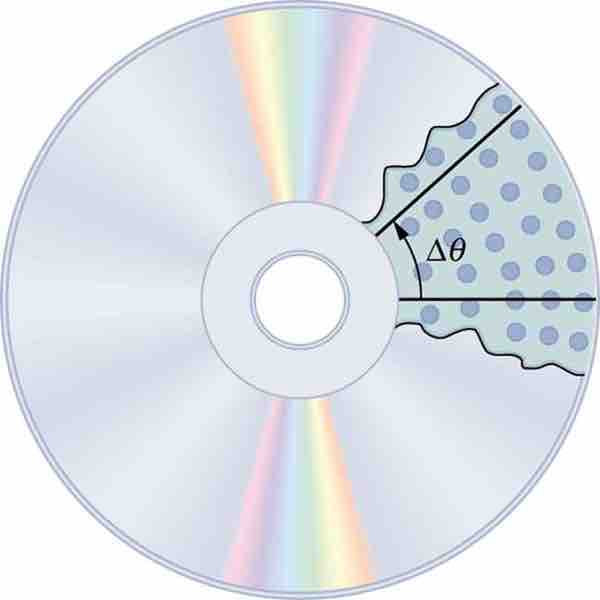
When objects rotate about some axis—for example, when the CD (compact disc) rotates about its center—each point in the object follows a circular arc. Consider a line from the center of the CD to its edge. Each pit used to record sound along this line moves through the same angle in the same amount of time. The rotation angle is the amount of rotation, and is analogous to linear distance. We define the rotation angle
Rotation Angle
All points on a CD travel in circular arcs. The pits along a line from the center to the edge all move through the same angle Δ in a time Δt.
In mathematics, the angle of rotation (or angular position) is a measurement of the amount (i.e., the angle) that a figure is rotated about a fixed point (often the center of a circle, as shown in ).
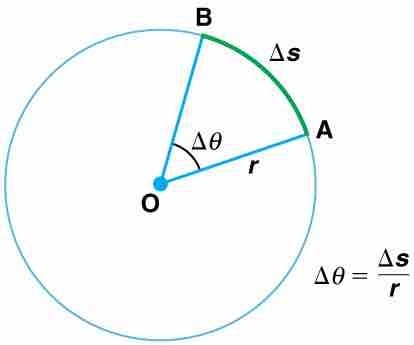
Angle θ and Arc Length s
The radius of a circle is rotated through an angle Δ. The arc length Δs is described on the circumference.
The arc length Δs is the distance traveled along a circular path. r is the radius of curvature of the circular path. We know that for one complete revolution, the arc length is the circumference of a circle of radius r. The circumference of a circle is 2πr. Thus, for one complete revolution the rotation angle is:
This result is the basis for defining the units used to measure rotation angles to be radians (rad), defined so that:
2π rad = 1 revolution.
If
1rad = 360º/2π = 57.3º.