Electric vs. Magnetic Forces
Force due to both electric and magnetic forces will influence the motion of charged particles. However, the resulting change to the trajectory of the particles will differ qualitatively between the two forces. Below we will quickly review the two types of force and compare and contrast their effects on a charged particle.
Electrostatic Force and Magnetic Force on a Charged Particle
Recall that in a static, unchanging electric field E the force on a particle with charge q will be:
Where F is the force vector, q is the charge, and E is the electric field vector. Note that the direction of F is identical to E in the case of a positivist charge q, and in the opposite direction in the case of a negatively charged particle. This electric field may be established by a larger charge, Q, acting on the smaller charge q over a distance r so that:
It should be emphasized that the electric force F acts parallel to the electric field E. The curl of the electric force is zero, i.e.:
A consequence of this is that the electric field may do work and a charge in a pure electric field will follow the tangent of an electric field line.
In contrast, recall that the magnetic force on a charged particle is orthogonal to the magnetic field such that:
where B is the magnetic field vector, v is the velocity of the particle and θ is the angle between the magnetic field and the particle velocity. The direction of F can be easily determined by the use of the right hand rule .
Right Hand Rule
Magnetic fields exert forces on moving charges. This force is one of the most basic known. The direction of the magnetic force on a moving charge is perpendicular to the plane formed by v and B and follows right hand rule–1 (RHR-1) as shown. The magnitude of the force is proportional to q, v, B, and the sine of the angle between v and B.
If the particle velocity happens to be aligned parallel to the magnetic field, or is zero, the magnetic force will be zero. This differs from the case of an electric field, where the particle velocity has no bearing, on any given instant, on the magnitude or direction of the electric force.
The angle dependence of the magnetic field also causes charged particles to move perpendicular to the magnetic field lines in a circular or helical fashion, while a particle in an electric field will move in a straight line along an electric field line.
A further difference between magnetic and electric forces is that magnetic fields do not net work, since the particle motion is circular and therefore ends up in the same place. We express this mathematically as:
Lorentz Force
The Lorentz force is the combined force on a charged particle due both electric and magnetic fields, which are often considered together for practical applications. If a particle of charge q moves with velocity v in the presence of an electric field E and a magnetic field B, then it will experience a force:
Electric and Magnetic Field Lines
We mentioned briefly above that the motion of charged particles relative to the field lines differs depending on whether one is dealing with electric or magnetic fields. There are some notable differences between how electric and magnetic field lines are conceptualized. The electric field lines from a positive isolated charge are simply a sequence of evenly-spaced, radially directed lines pointed outwards from the charge. In the case of a negative charge, the direction of the field is reversed. The electric field is directed tangent to the field lines. Of course, we imagine the field lines are more densely packed the larger the charges are. One can see clearly that the curl of the electric force is zero .
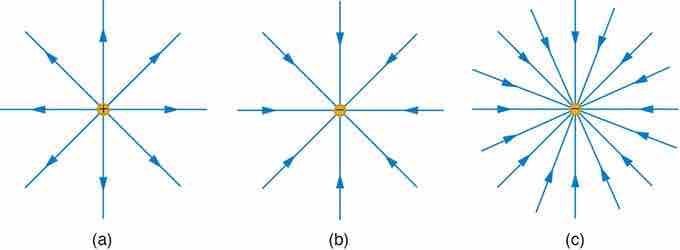
Electric Field Generated by Point Charges
The electric field surrounding three different point charges: (a) A positive charge; (b) a negative charge of equal magnitude; (c) a larger negative charge.
If multiple charges are involved, field lines are generated on positive charges, and terminate on negative ones.
In the case of magnets, field lines are generated on the north pole (+) and terminate on the south pole (-) - see the below figure. Magnetic 'charges', however, always come in pairs - there are no magnetic monopoles (isolated north or south poles). The curl of a magnetic field generated by a conventional magnet is therefore always non zero. Charged particles will spiral around these field lines, as long as the particles have some non-zero component of velocity directed perpendicular to the field lines .
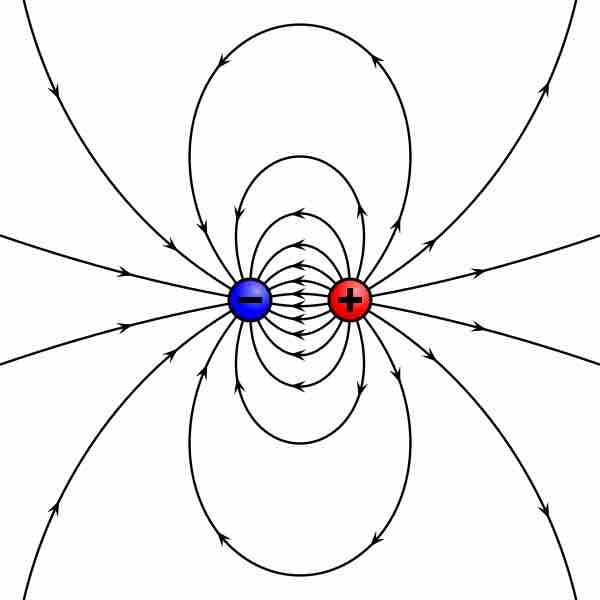
Magnetic Pole Model
The magnetic pole model: two opposing poles, North (+) and South (−), separated by a distance d produce an H-field (lines).
A magnetic field may also be generated by a current with the field lines envisioned as concentric circles around the current-carrying wire.The magnetic force at any point in this case can be determined with the right hand rule, and will be perpendicular to both the current and the magnetic field.