Constant Velocity Produces Straight-Line Motion
Recall Newton's first law of motion. If an object experiences no net force, then its velocity is constant: the object is either at rest (if its velocity is zero), or it moves in a straight line with constant speed (if its velocity is nonzero).
There are many cases where a particle may experience no net force. The particle could exist in a vacuum far away from any massive bodies (that exert gravitational forces) and electromagnetic fields. Or there could be two or more forces on the particle that are balanced such that the net force is zero. This is the case for, say, a particle suspended in an electric field with the electric force exactly counterbalancing gravity.
If the net force on a particle is zero, then the acceleration is necessarily zero from Newton's second law: F=ma. If the acceleration is zero, any velocity the particle has will be maintained indefinitely (or until such time as the net force is no longer zero). Because velocity is a vector, the direction remains unchanged along with the speed, so the particle continues in a single direction, such as with a straight line.
Charged Particles Moving Parallel to Magnetic Fields
The force a charged particle "feels" due to a magnetic field is dependent on the angle between the velocity vector and the magnetic field vector B . Recall that the magnetic force is:
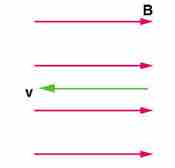
Zero Force When Velocity is Parallel to Magnetic Field
In the case above the magnetic force is zero because the velocity is parallel to the magnetic field lines.
If the magnetic field and the velocity are parallel (or antiparallel), then sinθ equals zero and there is no force. In this case a charged particle can continue with straight-line motion even in a strong magnetic field. If is between 0 and 90 degrees, then the component of v parallel to B remains unchanged.