de Broglie and the Wave Nature of Matter

In quantum mechanics, the concept of matter waves (or de Broglie waves) reflects the wave-particle duality of matter. The theory was proposed by Louis de Broglie in 1924 in his PhD thesis. The de Broglie relations show that the wavelength is inversely proportional to the momentum of a particle, and is also called de Broglie wavelength.

Einstein derived in his theory of special relativity that the energy and momentum of a photon has the following relationship:

$E = pc$ ($E$: energy, $p$: momentum, $c$: speed of light).

He also demonstrated, in his study of photoelectric effects, that energy of a photon is directly proportional to its frequency, giving us this equation:

$E = h \nu$ ($h$: Planck constant, $\nu$: frequency).

Combining the two equations, we can derive a relationship between the momentum and wavelength of light:

$p = \frac{E}{c} = \frac{h\nu}{c} = \frac{h}{\lambda}$. Therefore, we arrive at $\lambda = \frac{h}{p}$.

De Broglie's hypothesis is that this relationship $\lambda = \frac{h}{p}$, derived for electromagnetic waves, can be adopted to describe matter (e.g. electron, neutron, etc.) as well.

De Broglie didn't have any experimental proof at the time of his proposal. It took three years for Clinton Davisson and Lester Germer to observe diffraction patterns from electrons passing a crystalline metallic target (see ). Before the acceptance of the de Broglie hypothesis, diffraction was a property thought to be exhibited by waves only. Therefore, the presence of any diffraction effects by matter demonstrated the wave-like nature of matter. This was a pivotal result in the development of quantum mechanics. Just as the photoelectric effect demonstrated the particle nature of light, the Davisson–Germer experiment showed the wave-nature of matter, thus completing the theory of wave-particle duality.

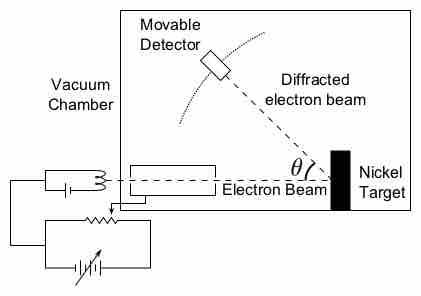
Davisson-Germer Experimental Setup

The experiment included an electron gun consisting of a heated filament that released thermally excited electrons, which were then accelerated through a potential difference (giving them a certain amount of kinetic energy towards the nickel crystal). To avoid collisions of the electrons with other molecules on their way towards the surface, the experiment was conducted in a vacuum chamber. To measure the number of electrons that were scattered at different angles, an electron detector that could be moved on an arc path about the crystal was used. The detector was designed to accept only elastically scattered electrons.

Experiments with Fresnel diffraction and specular reflection of neutral atoms confirm the application to atoms of the de Broglie hypothesis. Further, recent experiments confirm the relations for molecules and even macromolecules, normally considered too large to undergo quantum mechanical effects. In 1999, a research team in Vienna demonstrated diffraction for molecules as large as fullerenes. The researchers calculated a De Broglie wavelength of the most probable C₆₀ velocity as 2.5 pm.