Energy in a Magnetic Field

Magnetic field stores energy. The energy density is given as $u = \frac{\mathbf{B}\cdot\mathbf{B}}{2\mu}$.

Learning Objective

Express the energy density of a magnetic field in a form of equation

Key Points

Energy is needed to generate a magnetic field both to work against the electric field that a changing magnetic field creates and to change the magnetization of any material within the magnetic field.
For linear, non-dispersive, materials (such that B = μH where μ, called the permeability, is frequency-independent), the energy density is: $u = \frac{\mathbf{B}\cdot\mathbf{B}}{2\mu} = \frac{\mu\mathbf{H}\cdot\mathbf{H}}{2}$.
The energy stored by an inductor is $E_{stored} = \frac{1}{2}LI^2$.

Terms

inductor
A passive device that introduces inductance into an electrical circuit.
permeability
A quantitative measure of the degree of magnetization of a material in the presence of an applied magnetic field (measured in newtons per ampere squared in SI units).
ferromagnet
Materials that show a permanent magnetic property.

Full Text

Energy is needed to generate a magnetic field both to work against the electric field that a changing magnetic field creates and to change the magnetization of any material within the magnetic field. For non-dispersive materials this same energy is released when the magnetic field is destroyed. Therefore, this energy can be modeled as being "stored" in the magnetic field .

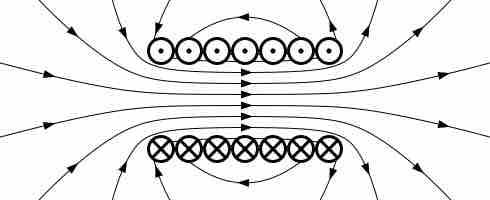
Magnetic Field Created By A Solenoid

Magnetic field created by a solenoid (cross-sectional view) described using field lines. Energy is "stored" in the magnetic field.

Energy Stored in a Magnetic Field

For linear, non-dispersive, materials (such that B = μH where μ, called the permeability, is frequency-independent), the energy density is:

$u = \frac{\mathbf{B}\cdot\mathbf{B}}{2\mu} = \frac{\mu\mathbf{H}\cdot\mathbf{H}}{2}$.

Energy density is the amount of energy stored in a given system or region of space per unit volume. If there are no magnetic materials around, μ can be replaced by μ₀. The above equation cannot be used for nonlinear materials, though; a more general expression (given below) must be used.

In general, the incremental amount of work per unit volume δW needed to cause a small change of magnetic field δB is:

$\delta W = \mathbf{H}\cdot\delta\mathbf{B}$.

Once the relationship between H and B is known this equation is used to determine the work needed to reach a given magnetic state. For hysteretic materials such as ferromagnets and superconductors, the work needed also depends on how the magnetic field is created. For linear non-dispersive materials, though, the general equation leads directly to the simpler energy density equation given above.

Energy Stored in the Field of a Solenoid

The energy stored by an inductor is equal to the amount of work required to establish the current through the inductor, and therefore the magnetic field. This is given by:

$E_{stored} = \frac{1}{2}LI^2$.

Proof: Power that should be supplied to an inductor with inductance L to run current I through it it given as

$P = VI = L\frac{dI}{dt} \times I$.

Therefore

$E_{stored} = \int_0^T P(t) dt = \int_0 ^I LI' dI' = \frac{1}{2} LI^2$.

[ edit ]

Prev Concept

Mechanical Work and Electrical Energy

Transformers

Next Concept