We learned about motional EMF previously (see our Atom on "Motional EMF"). For the simple setup shown below, motional EMF
where B is the magnetic field, l is the length of the conducting rod, and v is the (constant) speed of its motion. (B, l, and v are all perpendicular to each other as shown in the image below.)
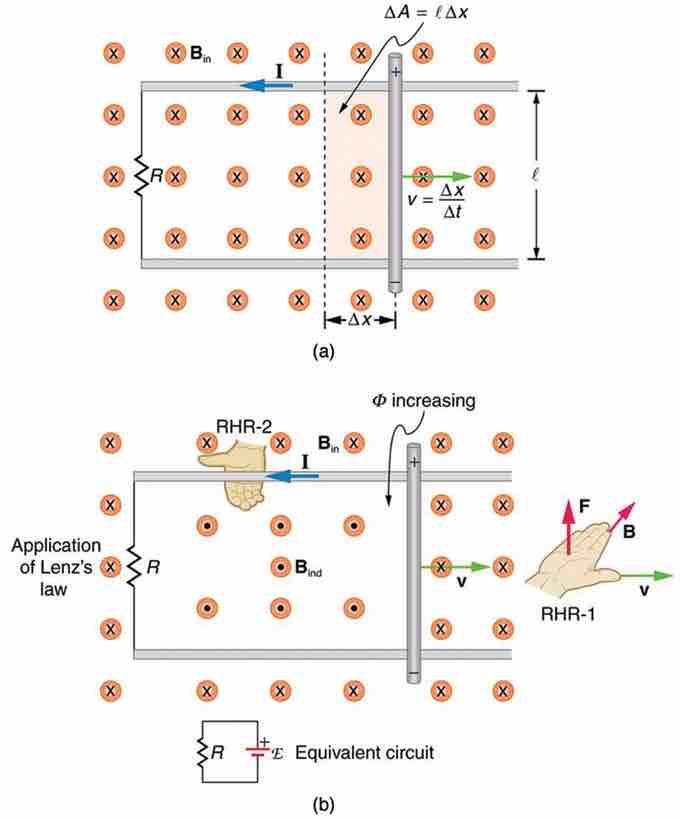
Motional EMF
(a) A motional emf=Bℓv is induced between the rails when this rod moves to the right in the uniform magnetic field. The magnetic field B is into the page, perpendicular to the moving rod and rails and, hence, to the area enclosed by them. (b) Lenz's law gives the directions of the induced field and current, and the polarity of the induced emf. Since the flux is increasing, the induced field is in the opposite direction, or out of the page. Right hand rule gives the current direction shown, and the polarity of the rod will drive such a current.
Conservation of Energy
In this atom, we will consider the system from the energy perspective. As the rod moves and carries current i, it will feel the Lorentz force
To keep the rod moving at a constant speed v, we must constantly apply an external force Fext (equal to magnitude of FL and opposite in its direction) to the rod along its motion. Since the rod is moving at v, the power P delivered by the external force would be:
In the final step, we used the first equation we talked about. Note that this is exactly the power dissipated in the loop (= current
Lenz' Law
We learned in the Atom "Faraday's Law of Induction and Lenz' Law" that Lenz' law is a manifestation of the conservation of energy. As we see in the example in this Atom, Lenz' law guarantees that the motion of the rod is opposed because of nature's tendency to oppose a change in magnetic field. If the induced EMF were in the same direction as the change in flux, there would be a positive feedback causing the rod to fly away from the slightest perturbation.