Resonance is the tendency of a system to oscillate with greater amplitude at some frequencies than at others. Frequencies at which the response amplitude is a relative maximum are known as the system's resonance frequencies. To study the resonance in an RLC circuit, as illustrated below, we can see how the circuit behaves as a function of the frequency of the driving voltage source.
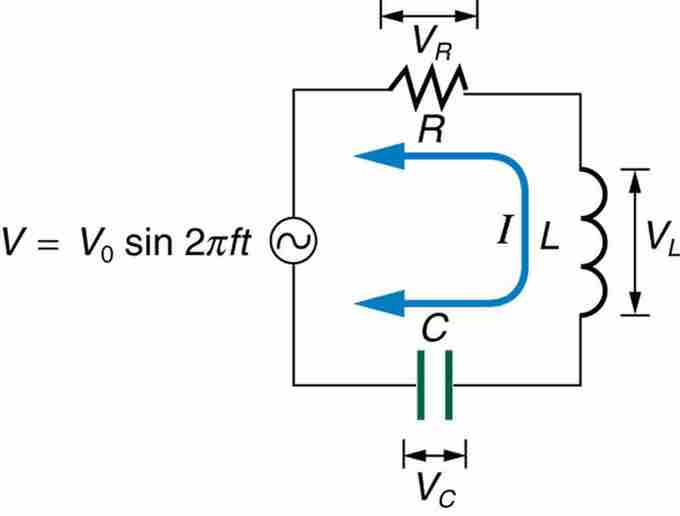
RLC Series Circuit
An RLC series circuit with an AC voltage source. f is the frequency of the source.
Combining Ohm's law, Irms=Vrms/Z, and the expression for impedance Z from
where Irms and Vrms are rms current and voltage, respectively. The reactances vary with frequency
At some intermediate frequency
The receiver in a radio is an RLC circuit that oscillates best at its
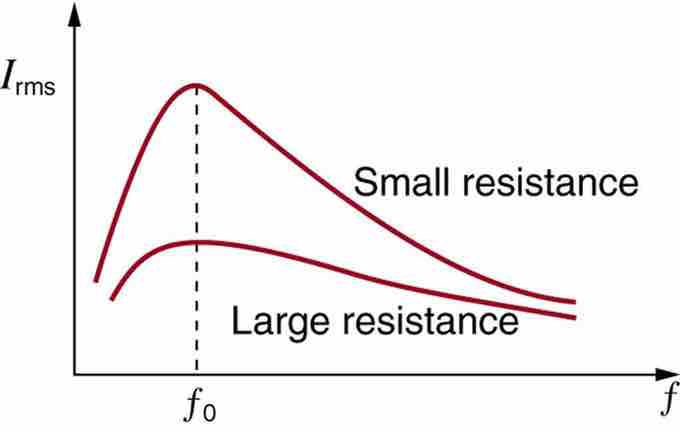
Current vs. Frequency
A graph of current versus frequency for two RLC series circuits differing only in the amount of resistance. Both have a resonance at f0, but that for the higher resistance is lower and broader. The driving AC voltage source has a fixed amplitude V0.