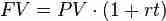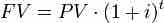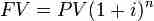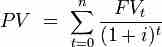Chapter 5
The Time Value of Money
By Boundless
Since the number of periods (n or t) is one, FV=PV(1+i), where i is the interest rate.
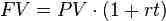
Multi-period investments take place over more than one period (usually multiple years). They can either accrue simple or compound interest.
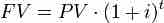
The Future Value can be calculated by knowing the present value, interest rate, and number of periods, and plugging them into an equation.
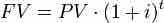
Calculating FV is a matter of identifying PV, i (or r), and t (or n), and then plugging them into the compound or simple interest formula.
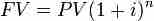
When considering a single-period investment, n is one, so the PV is simply FV divided by 1+i.
Multi-period investments require an understanding of compound interest, incorporating the time value of money over time.

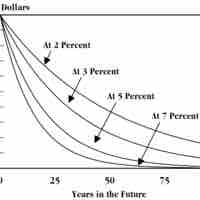
Discounting is the procedure of finding what a future sum of money is worth today.
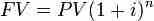
The number of periods corresponds to the number of times the interest is accrued.
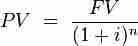
Calculating the present value (PV) is a matter of plugging FV, the interest rate, and the number of periods into an equation.
An annuity is a type of investment in which regular payments are made over the course of multiple periods.
The future value of an annuity is the sum of the future values of all of the payments in the annuity.
The PV of an annuity can be found by calculating the PV of each individual payment and then summing them up.
Understanding the relationship between each variable and the broader concept of the time value of money enables simple valuation calculations of annuities.
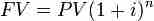
Present value (PV) and future value (FV) measure how much the value of money has changed over time.
The present value of a perpetuity is simply the payment size divided by the interest rate and there is no future value.
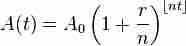
Finding the Effective Annual Rate (EAR) accounts for compounding during the year, and is easily adjusted to different period durations.
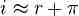
Variables, such as compounding, inflation, and the cost of capital must be considered before comparing interest rates.
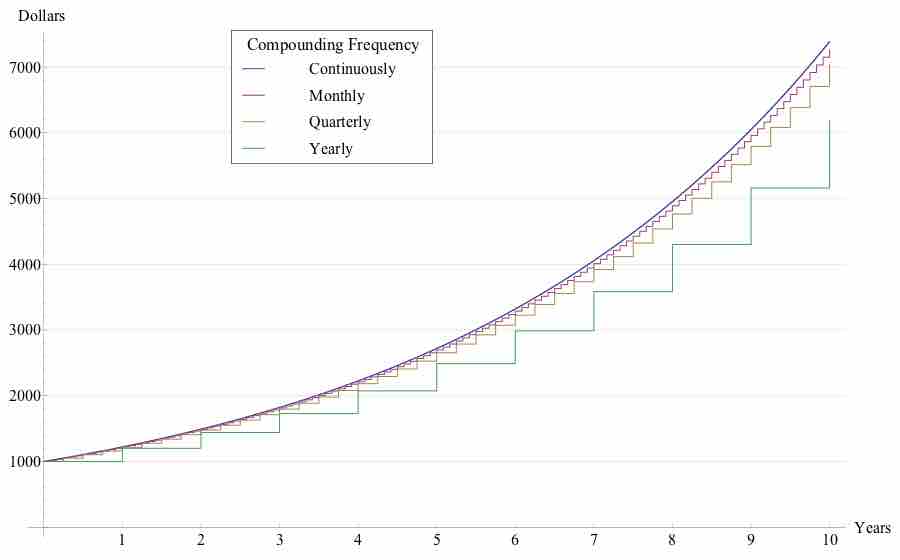
The value of money and the balance of the account may be different when considering fractional time periods.
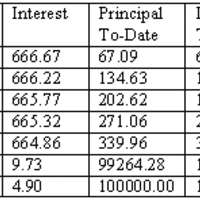
When borrowing money to be paid back via a number of installments over time, it is important to understand the time value of money and how to build an amortization schedule.
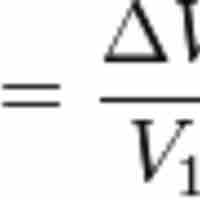
The yield of a single period investment is simply
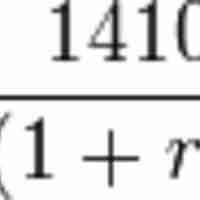
The yield of an annuity is commonly found using either the percent change in the value from PV to FV, or the internal rate of return.