Up to this point, we have implicitly assumed that the number of periods in question matches to a multiple of the compounding period. That means that the point in the future is also a point where interest accrues. But what happens if we are dealing with fractional time periods?
Compounding periods can be any length of time, and the length of the period affects the rate at which interest accrues.
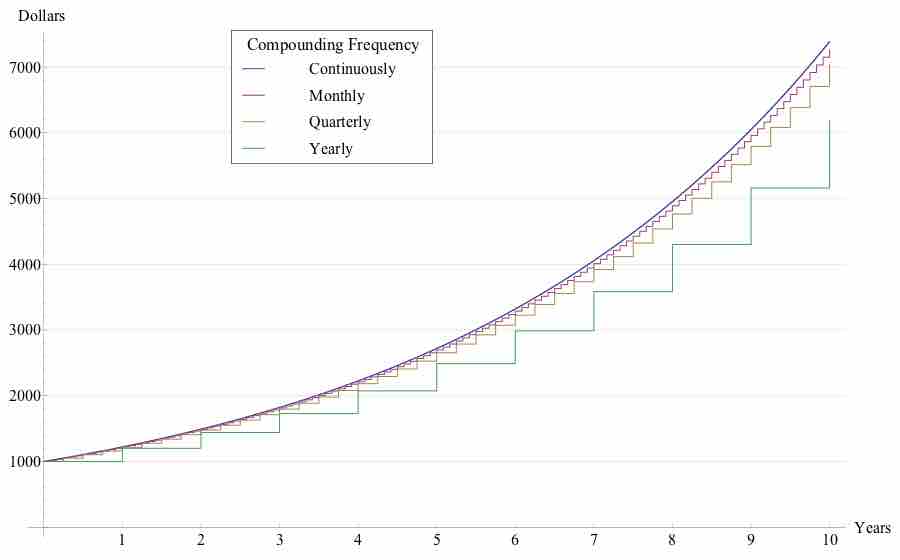
Compounding Interest
The effect of earning 20% annual interest on an initial $1,000 investment at various compounding frequencies.
Suppose the compounding period is one year, starting January1, 2012. If the problem asks you to find the value at June 1, 2014, there is a bit of a conundrum. The last time interest was actually paid was at January 1, 2014, but the time-value of money theory clearly suggests that it should be worth more in June than in January.
In the case of fractional time periods, the devil is in the details. The question could ask for the future value, present value, etc., or it could ask for the future balance, which have different answers.
Future/Present Value
If the problem asks for the future value (FV) or present value (PV), it doesn't really matter that you are dealing with a fractional time period. You can plug in a fractional time period to the appropriate equation to find the FV or PV. The reasoning behind this is that the interest rate in the equation isn't exactly the interest rate that is earned on the money. It is the same as that number, but more broadly, is the cost of not having the money for a time period. Since there is still a cost to not having the money for that fraction of a compounding period, the FV still rises.
Account Balance
The question could alternatively ask for the balance of the account. In this case, you need to find the amount of money that is actually in the account, so you round the number of periods down to the nearest whole number (assuming one period is the same as a compounding period; if not, round down to the nearest compounding period). Even if interest compounds every period, and you are asked to find the balance at the 6.9999th period, you need to round down to 6. The last time the account actually accrued interest was at period 6; the interest for period 7 has not yet been paid.
If the account accrues interest continuously, there is no problem: there can't be a fractional time period, so the balance of the account is always exactly the value of the money.