When lending money (or borrowing, depending on your perspective), it is common to have multiple payback periods over time (i.e. multiple, smaller cash flow installments to pay back the larger borrowed sum). In these situations, an amortization schedule will be created. This will determine how much will be paid back each period, and how many periods of repayment will be required to cover the principal balance. This must be agreed upon prior to the initial borrowing occurs, and signed by both parties.

Time Value of Money

Now if you add up all of the separate payments in an amortization schedule, you'll find the total exceeds the amount borrowed. This is because amortization schedules must take into account the time value of money. Time value of money is a fairly simple concept at it's core: a dollar today is worth more than a dollar tomorrow. 

Why? Because capital can be invested, and those investments can yield returns. Lending your money to someone means incurring the opportunity cost of the other things you could do with that money. This gets even more drastic as the scale of capital increases, as the returns on capital over time are expressed in a percentage of the capital invested. Say you spend $100 on some stock, and turn 10% on that investment. You now have $110, a profit of $10. Say instead of only a $100, you put in $10,000. Now you have $11,000, a profit of $1,000. 

Principle and Interest

As a result of this calculation, amortization schedules charge interest over time as a percentage of the principal borrowed. The calculation will incorporate the number of payment periods (n), the principal (P), the amortization payment (A) and the interest rate (r).

${\displaystyle P\,=\,A\cdot {\frac {1-\left({\frac {1}{1+r}}\right)^{n}}{r}}}$

To make this a bit more realistic, let's insert some numbers. Let's say you find a dream house, at the reasonable rate of $100,000. Unfortunately, a bit of irresponsible borrowing in your past means you must pay 8% interest over a 30 year loan, which will be paid via a monthly amortization schedule (12 months x 30 years = 360 payments total). If you do the math, you should find yourself paying $734 per month 360 times. 360 x 734 will leave you in the ballpark of $264,000 in total repayment. that means you are paying more than 2.5 times as much for this house due to time value of money! This bit of knowledge is absolutely critical for personal financial decisions, as well as for high level business decisions. 

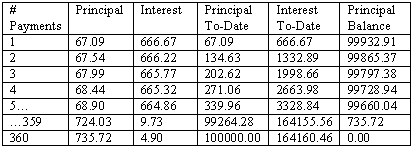
Amortization Schedule Example

This shows the first few installments in the example discussed above (i.e. borrowing $100,000 at 8% interest paid monthly over 30 years).

This shows the first few installments in the example discussed above (i.e. borrowing $100,000 at 8% interest paid monthly over 30 years).