There are several limits of special interest involving trigonometric functions.

1. $\displaystyle{\lim_{x \to 0} \frac{\sin x}{x} = 1}$

This limit can be proven with the squeeze theorem.

For $0 < x < \frac{ \pi}{2}$, $\sin x < x < \tan x.$

Dividing everything by $\sin x$ yields:

 $1 < \frac{x}{\sin x} < \frac{\tan x}{\sin x}$

which reduces to:

$\displaystyle{1 < \frac{x}{\sin x} < \frac{1}{\cos x}}$.

Taking the limit of the right-hand side: 

$\displaystyle{\lim_{x \to 0} \left ( \frac{1}{\cos x} \right ) = \frac{1}{1} = 1}$

The squeeze theorem tells us that:

$\displaystyle{\lim_{x \to 0} \left ( \frac{x}{\sin x} \right ) = 1}$

Equivalently:

$\displaystyle{\lim_{x \to 0} \left ( \frac{\sin x}{x} \right ) = 1}$

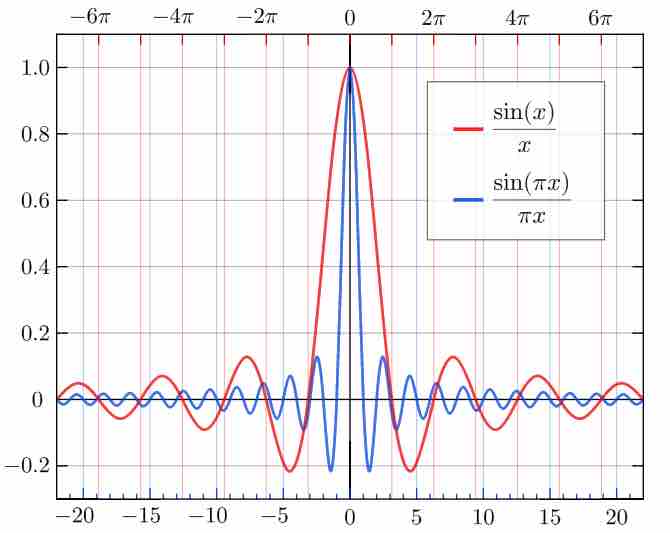
Sinc Function

The normalized sinc (blue, higher frequency) and unnormalized sinc function (red, lower frequency) shown on the same scale.

2. $\displaystyle{\lim_{x \to 0} \frac{1 - \cos x}{x} = 0}$

This equation can be proven with the first limit and the trigonometric identity $1 - \cos^2 x = \sin^2 x$.

We start with:

$\displaystyle{\frac{1 - \cos x}{x}}$

Multiplying the numerator and denominator by $1 + \cos x$,

$\displaystyle{\frac{(1−\cos x)(1+\cos x)}{x(1+\cos x)}=\frac{(1−\cos^2x)}{x(1+\cos x)}=\frac{\sin^2x}{x(1+\cos x)}= \frac{\sin x}{x} \cdot \frac{\sin x}{1+\cos x}}$

Using the algebraic limit theorem,

$\displaystyle{\lim_{x \to 0}\left ( \frac{\sin x}{x} \frac{\sin x}{1 + \cos x} \right ) = \left (\lim_{x \to 0} \frac{\sin x}{x} \right ) \left ( \lim_{x \to 0} \frac{\sin x}{1 + \cos x} \right ) = \left (1 \right )\left (\frac{0}{2} \right )= 0}$

Therefore:

$\displaystyle{\lim_{x \to 0} \frac{1 - \cos x}{x} = 0}$

3. $\lim_{x \to \infty} x \sin \left(\frac{c}{x}\right) = c$

This relation can be proven by substituting $t=\frac{1}{x}$ into the first relation we derived:

$\displaystyle{\lim_{t \to 0} \left ( \frac{\sin t}{t} \right ) = 1}$.