Finding Limits Algebraically

If $f$ is a real-valued (or complex-valued) function, then taking the limit is compatible with the algebraic operations, provided the limits on the right sides of the equations below exist (the last identity holds only if the denominator is non-zero). This set of rules is often called the algebraic limit theorem, expressed formally as follows:

$\displaystyle{\begin{matrix} \lim\limits_{x \to p} & (f(x) + g(x)) & = & \lim\limits_{x \to p} f(x) + \lim\limits_{x \to p} g(x) \\ \lim\limits_{x \to p} & (f(x) - g(x)) & = & \lim\limits_{x \to p} f(x) - \lim\limits_{x \to p} g(x) \\ \lim\limits_{x \to p} & (f(x)\cdot g(x)) & = & \lim\limits_{x \to p} f(x) \cdot \lim\limits_{x \to p} g(x) \\ \lim\limits_{x \to p} & \left ( \frac{f(x)}{g(x)} \right ) & = & \frac{\lim\limits_{x \to p} f(x)} {\lim\limits_{x \to p} g(x)} \end{matrix}}$

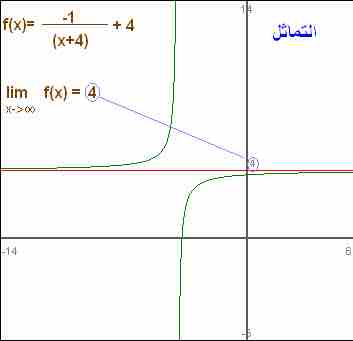
Finding a Limit

The limit of $f(x)= \frac{-1}{(x+4)} + 4$ as $x$ goes to infinity can be segmented down into two parts: the limit of $\frac{−1}{(x+4)}$ and the limit of $4$. The former is $0$, while the latter is $4$. Therefore, the limit of $f(x)$ as $x$ goes to infinity is $4$.

In each case above, when the limits on the right do not exist (or, in the last case, when the limits in both the numerator and the denominator are zero), the limit on the left, called an indeterminate form, may nonetheless still exist—this depends on the functions f and g. These rules are also valid for one-sided limits, for the case $p = \pm$, and also for infinite limits using the following rules:

$\displaystyle{\begin{matrix} &q + \infty &=& \infty \text{ for } q \neq - \infty \\ &q \cdot \infty &=& \infty \text{ if } q > 0 \\ &q \cdot \infty &=& -\infty \text{ if } q < 0 \\& \frac{q}{\infty} &=& 0 \text{ if } q \neq \pm \infty \end{matrix}}$

Note that there is no general rule for the case $\frac{q}{0}$; it all depends on the way $0$ is approached. Indeterminate forms—for instance, $\frac{0}{0}$, $0 \cdot$ some number, $\infty$, and $\frac{\infty}{\infty}$ are also not covered by these rules, but the corresponding limits can often be determined with L'Hôpital's rule or the squeeze theorem. We will study these rules in the following atoms.